1.3 The Standard View
This module introduces key concepts that are part of the “Standard View” in philosophy, which form the foundations for logic. These concepts include representation, accuracy, facts, sentences, propositions, truth, negation, and logical connectives.
Many people bring their own pre-conceived notions about what these words mean. Often, the way that these terms are used differs from the specialized meanings these words have among philosophers.
Table of Contents
- 1.3 The Standard View
1.3.1 Representations

An artist’s portrait of a cityscape represents the real city scape in the background.
Representations
We will now turn from giving an overview of what we’ll be studying in the course, to presenting some basic concepts that are useful to have before a study of logic. These concepts are not difficult. In fact, you have them already and probably rely on them every day. There is a particular way of thinking about these concepts which will be useful for studying logic, however. We will call the view presented over the next few pages the standard view. There are other philosophy courses one might take which challenge the standard view, but for this course we will assume the standard view.
The most basic concept on the standard view is that of a representation. A representation is something which stands for or is about something else, and which can be accurate or inaccurate about it. Pictures, maps, diagrams, text, numbers, and even the sound of a fire alarm or the smell of perfume are all representations: they are about something besides themselves. For instance, when you want to give somebody directions, you might draw a line on a piece of paper to represent the route they should take, and other lines to represent streets, or simple pictures to represent landmarks.
In this example, your drawing is accurate if the route is indeed as you represent it, and your drawing is inaccurate if because of it the person is lead wildly astray from their destination, because the route is nothing like how you drew it.
Accuracy
On the standard view, what makes a representation accurate or inaccurate we call reality or the world. By “the world”, we don’t mean planet earth necessarily, but we mean just that part of reality which makes our representations accurate or inaccurate. (Maybe there are some things which are real, but which we can’t represent in words, or in any other way). A representation is accurate if it corresponds to reality, and a representation is inaccurate when it fails to correspond to reality. The important thing to remember is that a representation is to be evaluated by whether or not it is accurate about what it aims to represent.
In a logic class, the type of representation we focus on is our language. The most important part of language for the purposes of logic is a sentence. Sentences provide representations of the world, much like pictures do. When sentences accurately represent the world, they are true, and when they inaccurately represent the world, they are false.
Note: There should be two exercises below.
The first exercise asks you which are typically representations. For this exercise, you are to consider the thing referred to by the words and pictured by the image, not the image itself. (The image is, obviously, a representation — the question is about what the image pictures). For example, if you see a picture of a cow and the words “a cow”, the question is asking whether a cow is typically a representation, not whether the picture represents a cow.
The second exercise asks you whether the image itself is an accurate or inaccurate representation. In this case, you are to think not of the thing named by the image, but the image itself and whether it represents what it refers to correctly or not. For example, if you see a picture of a cow, you should ask whether the picture gets most of the important features of real cows right, or whether it is wrong in significant ways about what a cow looks like (it has eight tentacles and three heads).
1.2 Facts

That the earth is a sphere is the fact which makes it true that “The earth is a sphere.”
Facts as States of Affairs
The statement, “There are two chairs in my living room” is true. This statement is true because it accurately represents the world. There is something specific within the world, however, which makes it true. What makes this sentence true, for example, has nothing to do with the solar system or guacamole. Both the solar system and guacamole are parts of the world, but they are not what make the sentence true. Instead, what makes this sentence true has to do with two particular objects, my chairs, and their particular location, in my living room.
The specific part of a world which makes a statement true we call a fact or a state of affairs. (These mean the same thing). The state of affairs of my two chairs being located in my living room is what makes the sentence, “There are two chairs in my living room” true. Likewise, what make the sentence “Washington D.C. is the Capital of the USA” true is the fact that Washington D.C. is the capital of the USA.
For every claim or proposition, either there exists some fact or state of affairs which makes the claim true, or there doesn’t exist such a fact or state of affairs, and the claim is false. For example, “American money is made from animal hides” is a claim. For this claim to be true, there would have to be a state of affairs in our world where American money was being made out of animal hides. Our world does not contain this state of affairs, however. So, the claim is false.
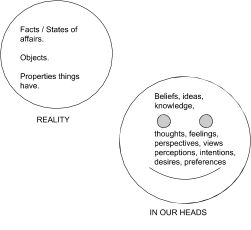
Facts are in the world, not in our heads. Facts are parts of reality, not parts of our way of thinking about reality. For example, it is a fact that the ocean is full of water. I have in my head a certain picture of the ocean, and that picture can be accurate or inaccurate, but the picture inside my head when I imagine the ocean is not the same thing as the ocean. Whether I imagine the ocean correctly as full of water or incorrectly as full of orange juice, how I imagine it is not the fact. The fact that the ocean is full of water is independent of me and how I think about it.
Clarifying the Term ‘Fact’
Sometimes, when people use the word “fact”, they use it as a tool to try to shut down conversation, or to try to declare something settled. For example, people often say that something is a “fact” if they want to emphasize that they are very confident that it is the case, or that they know it is the case, or that they believe others ought to know that it is the case.
Another way people misuse the word “fact” is to deny that something is a fact if they don’t know it to be the case, or if it is very hard to know whether it is the case, if they lack a quantifiable or measurable method of determining that it is the case.
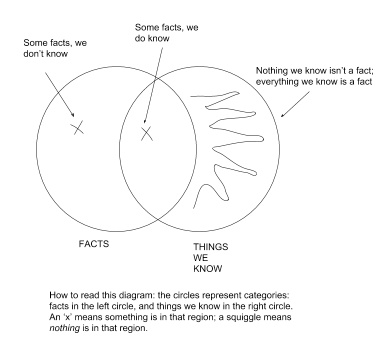
Both of these misuses of the word “fact” neglect the difference between being a fact and being something we know. Although everything we know is a fact, there are many facts which we don’t know. For example, we don’t know how many coyotes there are in Arizona, and whether the number of coyotes in Arizona is currently an even number or an odd number. Either it is a fact that the number of coyotes in Arizona is even, or else it is a fact that the number of coyotes in Arizona is odd. No one knows either way, however.
1.3.3 Sentences and Propositions
A diagram of the subject and predicate of a sentence.
Subject-Predicate Structure
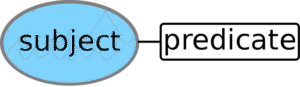
Sentences have a Subject-Predicate Structure. The predicate of a sentence attributes some property to the subject of the sentence. The subject of a sentence is a noun phrase, typically some person, place, thing, or idea, which the sentence is about, and to which the sentence attributes the property in the predicate.
For example, in the sentence “The old man is washing the dishes in the bathtub”, the subject of the sentence is the noun phrase:
The old man
And the sentence attributes to the old man the property in the predicate:
is washing the dishes in the bathtub.
Again, in the sentence “Television died after Seinfeld ended,” the subject of the sentence is the abstract noun:
Television
And the sentence attributes to Television the property in the predicate:
died after Seinfeld ended.
In nearly all declarative sentences in English, the subject is first, and the predicate follows the subject. Nonetheless, there are some exceptions. For example, in the sentence, “Fearlessly and carelessly ran the two children, over the hill and to the village”, the subject is:
The two children
And the predicate is:
Fearlessly and carelessly ran over the hill and to the village
Declarative Sentences
Sentences are usually categorized into four kinds. The first three kinds of sentences will not be of interest to us in this course, because they are neither true nor false.
- Interrogative sentences pose questions.
- For example, “Are you awake?” is an interrogative sentence, as is “What is the latest update?”.
- Questions are neither true nor false.
- Imperative sentences issue commands, requests, or advice.
- For example, “Go away!”, or “Please pass the salt”, or “Stay off University Drive during Rush Hour” are all imperative sentences.
- In English, we indicate an imperative sentence by dropping the subject of the sentence. The subject of an imperative sentence is implied to be you, but we don’t normally say, “Go away, you!”, just “Go away!”
- Imperatives are neither true nor false.
- Exclamatory sentences express a feeling.
- For example, “Yay!” or “Go ASU!” are both exclamatory sentences.
- Exclamatory sentences are neither true nor false.
Although some philosophers have attempted to develop systems of logic for these kinds of sentences, our interest will be in the fourth kind of sentence:
- Declarative sentences are used to assert or describe the world
- For example, “Harry Truman lived to be 107 years old“, or “Cheating is wrong” are both declarative sentences.
- Most declarative sentences are either true, or else they are false.
- “Harry Truman lived to be 107 years old” is false.
- “Cheating is wrong” is true.
- A few very strange declarative sentences are neither true nor false. For example, the sentence “This sentence is false” is neither true nor false. We will ignore these sentences in our class, but more advanced logic courses address them.
Declarative sentences which are either true or false are called statements. Every statement is either true, or else it is false. A statement is true when it represents the world accurately, and it is false when it represents the world inaccurately. For example, the declarative sentence “Some cats meow” is a statement. This statement is true, because in fact some cats do meow. The declarative sentence “Some dogs fly using their tails” is a statement. This statement is false, because in fact no dogs fly using their tails. On the other hand, the sentence “Go dogs, go!” is not a statement, because it is not a declarative sentence. Statements express propositions.
Propositions
We will say that a statement makes a claim about the world, which is either true or false of the world. The claim that a statement makes is also called a proposition. Although in English we sometimes use the world “proposition” to mean a “proposal”, in logic we use “proposition” to mean the claim that someone makes about the world, which is either true or false about the world.
Two different statements can express the same proposition. In other words, two different declarative sentences can make the same claim about the world. For example, two statements which use synonyms, or words that mean the same thing, can express the same proposition despite using different words. Here are two sentences which say the same thing about Sherlock Holmes:
Sherlock bought the big fish eggs fast.
Mr. Holmes purchased the large roe speedily.
These are two different sentences, but they make the same claim about the world, and would be true or false in all of the same possible situations. So, these two sentences express the same proposition. Similarly, two different sentences in different languages might express the same proposition, as these two sentences do:
I need help.
Necesito ayuda.
The sentence in Spanish, “necesito ayuda”, expresses the same proposition as the sentence in English, “I need help.”
Two different propositions can be expressed by the same sentence. Some sentences are ambiguous, meaning they have multiple meanings. For example, consider the sentence:
Chloe went to the bank.
This sentence could mean that Chloe went to the edge of a river, or it could mean that Chloe went to a financial institution. Those are two different claims about the world, and two different propositions.
1.3.4 Truth and Propositions

Propositions are claims, which are true when they accurately represent the facts.
Propositions are true when they correspond to the facts. Propositions are false when they fail to correspond to the facts. For example:
- It is a fact that a normal hydrogen atom contains one proton and one electron.
- So, the proposition expressed by “a normal hydrogen atom contains one proton and one electron” is true.
- On the other hand, the proposition expressed by “a normal hydrogen atom contains no protons and two electrons” is false.
- It is a fact that the U. S. Declaration of Independence was written in 1776.
- So, the proposition expressed by “The U. S. Declaration of Independence was written prior to 1800” is true.
- On the other hand, the proposition expressed by “The U. S. Declaration of Independence was written after 1800” is false.
- It is a fact that Joe has lived a rather disappointing life.
- So, the proposition expressed by “Someone has lived a rather disappointing life” is true.
- On the other hand, the proposition expressed by “Nobody has lived a rather disappointing life” is false.
- It is a fact that every mammal is a vertebrate.
- So, the proposition expressed by “No mammals are invertebrates” is true.
- On the other hand, the proposition expressed by “Some invertebrates are mammals” is false.
As you can see, one fact can make many propositions true, and many propositions false. The fact that I eat eggs (that is, the state of the affairs in our world in which sometimes I eat eggs) makes true the proposition expressed by “The author of this sentence eats eggs”, as well as the propositions expressed by “Somebody eats eggs”, “Eggs are eaten”, and “I eat things”. In logic, we say that the fact that I eat eggs entails that these propositions are true. There is no way that they could be false if I eat eggs. Meanwhile, the fact that I eat eggs makes false the propositions expressed by “I don’t eat eggs”, “I don’t exist”, “I don’t eat anything”, and “nothing eats eggs”. Again, we would say the fact that I eat eggs entails that these propositions are false. There is no way that they could be true if I eat eggs.
Meanwhile, there are some propositions whose truth or falsity is not entailed by the fact that I eat eggs. For instance, the truth of “Eggs are inexpensive” or the falsity of “Slovakia is in South America” are not related to, and not entailed by, the fact that I eat eggs. Likewise, the fact that I eat eggs does not entail that it is false that “I am concerned by factory farming practices”, and it does not entail that it is true that “I think eggs are tasty.” These things might be suggested by the fact that I eat eggs, but they are not entailed by that fact.
It is important to think carefully about what a fact entails is true, what a fact entails is false, and what is not entailed by a fact.
1.3.5 Logical Connectives

Logical connectives include “And”, “Or”, and “If Then”
Logical Connectives
Every simple statement or proposition can be combined with any other in order to form a complex statement or proposition. For example, here are two simple statements:
Larry longs for lasagna.
Klor craves cabbage.
We can combine these into complex statements like:
Larry longs for lasagna OR Klor craves cabbage.
Larry longs for lasagna AND Klor craves cabbage.
IF Larry longs for lasagna THEN Klor craves cabbage.
We call the words “or”, “and”, and “if_then” logical connectives. The truth of complex statements or proposition depends on their parts and the logical connectives which are used to link them together. For example, what’s the difference between these two statements?
Larry longs for lasagna OR Klor craves cabbage.
Larry longs for lasagna AND Klor craves cabbage.
The first statement with the word ‘or’, would be true so long as in fact Klor craves cabbage, even if in fact Larry does not long for lasagna; it would also be true provided that in fact Larry longs for lasagna, even if Klor does not crave cabbage. The second statement, on the other hand, is only true when BOTH facts exist, both the fact that Larry longs for lasagna and the fact that Klor craves cabbage.
Another way in which we can make a complex proposition is by adding the word NOT to another proposition. This is called negation. For example, consider the proposition expressed by:
(+) Jamie has too much on her plate to care about food.
The negation of this proposition would be expressed by:
(~) Jamie does NOT have too much on her plate to care about food.
The negative is false whenever the positive form of the statement is true, and the positive form is false whenever the negative is true. If in fact Jamie has too much on her plate to care about food, then (+) is true and (-) above is false. If in fact Jamie does not have too much on her plate to care about food, then (+) is false and (-) is true. Notice that (+) and (-) will never both be true at the same time. If one is true, the other must be false.
We will study the ways to combine statements to form complex statements in this class, and the different ways in which the truth of simple statements determines the truth of complex statements.
Submodule 1.3 Quiz
Licenses and Attributions
Key Sources:
- Watson, Jeffrey (2019). Introduction to Logic. Licensed under: (CC BY-SA).
Next Page: 1.4 Rational Opinions
