6.4 Practice with Universals and Existentials
This module provides practice using Venn Diagrams to verify rules of inference, and applying the rules for Categorical Syllogism. It also introduces the Quantifier Negation law.
Table of Contents
6.4.1 Three Valid Forms of Categorical Syllogism
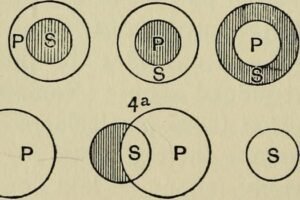
Possible relationships between a predicate and a subject.
The first two exercises below ask you to match each argument with a Venn Diagram of the premises. You will then use this information to answer the questions in the third exercise, so keep track of your answers.
6.4.2 Three Valid Forms of Categorical Syllogism

Augustus De Morgan, whose law is the basis for the Quantifier Negation laws.
Quantifier Negation Laws (QN)
Earlier, we introduced the following Contradictories in the Square of Opposition:
All S are P ← CONTRADICTS → Some S are not P
No S are P ← CONTRADICTS → Some S are P
We can now prove a distinct but equally interesting pair of logically equivalent categorical statements, known as the quantifier negation laws:
No S are P ≡ All S are non-P
Not All S are P ≡ Some S are not P
Whenever we have one side of the equivalence, we can infer the other side of the equivalence, citing the rule (QN) for Quantifier Negation:
- No S are P
- All S are non-P (1 QN)
- All S are non-P
- No S are P (1 QN)
- Not All S are P
- Some S are not P (1 QN)
- Some S are not P
- Not All S are P (1 QN)
Remembering that existentials are unlimited disjunctions, and universals are unlimited conjunctions, the quantifier negation laws are really an extension of DeMorgan’s laws in propositional logic:
~(S1 is P v S2 is P v …) ≡ ~(S1 is P) & ~(S2 is P) & …
~(S1 is P & S2 is P & …) ≡ ~(S1 is P) v ~(S2 is P) v …
6.4.3 Three Valid Forms of Categorical Syllogism

Students in Medieval Universities invented the nicknames for syllogisms.
Submodule 6.4 Quiz
Licenses and Attributions
Key Sources:
- Watson, Jeffrey (2019). Introduction to Logic. Licensed under: (CC BY-SA).
Next Page: 7.1 Review of Prior Modules 1-6
