6.2 Rules for Universals and Existentials
In this submodule, we discuss some of the most basic rules available for dealing with Universals and Existentials. First, we introduce two very basic rules: the rule of existential generalization, and the rule of applied universal instantiation. These rules express the basic meaning of what a “existential” or “universal” claim is.
Next, we discuss some of the “immediate inference” which we can easily see through looking at a truth table, through the rules of Contraposition, Obversion, and Conversion. We then turn to the law of identity and the law of the indiscernibility of identicals.
Lastly, we introduce the notion of an arbitrary variable, and see how it is used in the rule of existential instantiation. By the end of this module, we should have enough of the basics in place to begin considering the rules of categorical syllogism in the next module.
Table of Contents
- 6.2 Rules for Universals and Existentials
6.2.1 Basic Rules for Universals and Existentials
Some states don’t observe Daylight Savings Time.
Just as we can use Venn Diagrams to demonstrate that particular arguments are valid, we can also use them to demonstrate that certain general rules of inference are valid. The first two rules we’ll study for dealing with categorical statements we’ll call applied universal instantiation and existential generalization.
Applied Universal Instantiation (AUI)
If everyone at the party is having fun, and Olaf is at the party, then Olaf is having fun. If all cats meow, and Perkins is a cat, then Perkins meows. If everyone I’ve ever met has serious personal problems, and I’ve met Drew, then Drew has serious personal problems. If all people are going to die, and I’m a person, then I’m going to die. This common sense pattern of inference we will call the rule of “Applied Universal Instantiation”. We’re basing this rule on a more formal rule known as “Universal Instantiation”, which is studied in more advanced logic courses.
The rule looks like this, where S and P stand for categories, and x is a variable that stands for any particular thing.
- All S are P
- x is S
- x is P (1, 2 AUI)
We can use Venn Diagram to prove that this is form of argument is valid. We represent premise one by shading in all of the area in S outside of its intersection with P. We then represent premise 2 by marking an ‘x’ within S in the only space remaining, which is in the intersection with P. It follows that our ‘x’ is within P.

Existential Generalization (EG)
If Brad won the lottery, then somebody won the lottery. If the house is on fire, then something is on fire. If Meghan flew the plane, then something was flown by Meghan. If George is farmer who drinks goat’s milk, then some farmers drink goat’s milk. All of these inferences follow from the rule of existential generalization.
The rule looks like this, where S and P stand for categories, and x is a variable that stands for any particular thing.
- x is S
- Something is S (1 EG)
or
- x is S
- x is P
- Some S are P (1, 2 EG)
or
- x is S & x is P
- Some S are P (1, EG)
For instance:
- Arizona is a U. S. State.
- Arizona doesn’t observe daylight savings time.
- Some U. S. States don’t observe daylight savings time.
6.2.2 Conversion, Obversion, and Contraposition
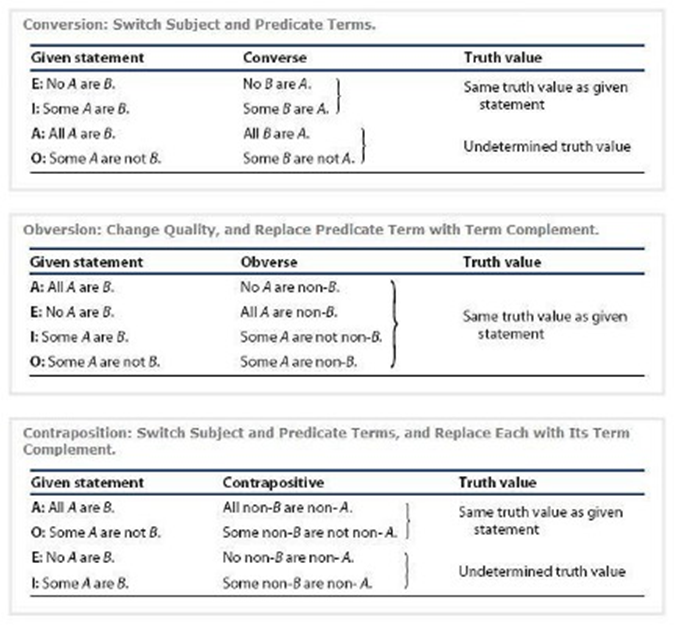
This chart summarizes the rules of conversion, obversion, and contraposition, as they are discussed on this page. Conversion switches the subject and predicate terms, and is valid for E (No A are B) and I (Some A are B) sentences, producing “No B are A” and “Some B are A” respectively. Conversion has an undetermined truth value and is not valid for A (All A are B) and O (some A are not B) sentences. Obversion changes the quality of the sentence, and replaces the predicate term with its complement. It is valid for all sentences: A (All A are B) becomes No A are non-B; E (No A are B) becomes All A are non B, I (Some A are B) becomes Some A are not non-B, and O (some A are not B) becomes Some A are non-B. Contraposition switches the subject and predicate terms, and replaces each with its term complement. It is invalid for E (No A are B) and I (some A are B) sentences, but valid for A (All A are B) and O (Some A are not B) sentences, where it produces “All non-B are non-A” and “some non-B are not non-A”, respectively.
Four Categories of Categorical Propositions
Recall that earlier we divided universals and existentials into four categories, and presented the square of opposition to display which one were contradictory to the others. There is a traditional medieval system for abbreviating these categories using the first four vowels (A, E, I, O), which happen to be the four vowels in the name “Aristotle”, which we’ll introduce below:
- A. Universal Affirmatives. All S are P. (“All of my friends are hardworking.”)
- E. Universal Negatives. No S are P. (“None of my friends are hardworking.”)
- I. Particular Affirmatives. Some S are P. (“Some of my friends are hardworking.”)
- O. Particular Negatives. Some S are not P. (“Some of my friends are not hardworking.”)
In addition to the fact that E propositions and I propositions contradict, and A propositions and O propositions contradict, there are other logical relationships which these types of sentences have to one another. These are expressed by the rules of conversion, obversion, and contraposition.
Conversion (CONV)
“Conversion” is when we switch the order of subject and predicate in a categorical sentence: when we switch from “S are P” to “P are S”. For instance, when we switch from “Some cats are animals” to “some animals are cats”. This switching in order is a valid rule of inference for E and I sentences (“CONV”), but the same switch in order is not valid for A or O sentences. We can prove this using Venn Diagrams.
E. Universal Negatives – Conversion is VALID
1. No S are P 2. No P are S (1 CONV)
For example:
1. No cats are birds.2. No birds are cats (1 CONV)

E Sentences: No S are P; so, no P are S
I. Particular Affirmatives – Conversion is VALID
1. Some S are P 2. Some P are S (1 CONV)
For example:
1. Some cats eat birds. 2. Some bird-eaters are cats. (1 CONV)

I Sentences: Some S are P; so, some P are S
A. Universal Affirmatives – Conversion is INVALID
1. All S are P.2. All P are S. !!INVALID!!
For example:
1. All cats are animals. 2. All animals are cats. !!INVALID!!

A Sentences: All S are P
O. Particular Negatives – Conversion is INVALID
1. Some S are not P. 2. Some P are not S. !!INVALID!!
For example:
1. Some birds are not pigeons. 2. Some pigeons are not birds. !!INVALID!!

O Sentences: Some S are not P
Obversion (OBV)
“Obversion” is similar to the rule of double negation. It involves making two “negative” changes to the proposition: first, changing from affirmative to negative or from negative to affirmative, and second either adding or subtracting a negation from the predicate. Here is what the rule looks like for each type of sentence:
- A. All S are P → No S are not P
- E. No S are P → All S are non-P
- I. Some S are P → Some S are not non-P
- O. Some S are not P → Some S are non-P
The rule of obversion is valid for every type of sentence. The rule is not very interesting for I or O sentences, but it is worth showing examples for A and E sentences. Again, we can prove these inferences valid using a Venn Diagram.
E. Universal Negatives – Obversion is VALID

E Sentences: No S are P; so, All S are non-P.
1. No S are P 2. All S are non-P (1 OBV)
For example:
1. No cats are birds. 2. All cats are non-birds (1 OBV)
…
A. Universal Affirmatives – Obversion is VALID

A Sentences: All S are P; so No S are not P
1. All S are P. 2. No S are not P. (1 OBV)
For example:
1. All cats are animals. 2. No cats are not animals. (1 OBV)
Contraposition of Categoricals (CTRA-CG)
Lastly, the rule of contraposition for categorical sentences involves a combination of conversion and double negation: first, the order of the subject and predicate is switched, from “S are P” to “P are S”; second, both S and P are negated. So, “S are P” because “non-P are non-S”. For instance, “All cats are animals” becomes “All non-animals are non-cats”. Contraposition is valid for A and O sentences. We can prove this using Venn Diagrams.
A. Universal Affirmatives – Contraposition is VALID

A Sentences: All S are P; so, All non-P are non-S
1. All S are P. 2. All Non-P are Non-S. (1, CTRA-CG)
For example:
1. All cats are animals. 2. All non-animals are non-cats. (1, CTRA-CG)
…
O. Particular Negatives – Contraposition is VALID

Some S are not P; so, Some non-P are not non-S
1. Some S are not P. 2. Some non-P are not non-S. (1 CTRA-CG)
For example:
1. Some birds are not pigeons. 2. Some non-pigeons are not non-birds. (1, CTRA-CG) 3. Some non-pigeons are birds. (2, DN)
The rule of contraposition is invalid for E sentences, however.
E. Universal Negatives – Contraposition is INVALID
1. No S are P 2. No non-P are non-S !!INVALID!!
For example:
1. No cats are birds. 2. No non-birds are non-cats !!INVALID!! (e.g., dogs are non-birds as well as non-cats)
In other words, the rule of contraposition is invalid for E-sentences so long as there are at least 3 properties in the world which a thing might have none of which fully overlaps with the other. (See “Q” on the Venn Diagram).

No S are P; but some Q might still be non-P and non-S
The rule of contraposition is also invalid for I-sentences:
I. Particular Affirmatives – Contraposition INVALID
1. Some S are P 2. Some non-P are non-S !!INVALID!!

Some S are P; but it doesn’t follow that some non-P are non-S
Note: it is difficult to offer a clear and uncontroversial counterexample which shows why it this rule is invalid for I sentences. After all, for the conclusion to be true, there need only be some category Q which doesn’t fully overlap with either S or P and which has at least one element in it which is neither in S nor P. So, proving the form of argument is invalid requires the possibility of a pair of properties, S and P, where at least some S are P, and where nothing is neither S nor P. Because giving a clear counterexample would require discussing issues in the philosophy of language and metaphysics that go beyond the scope of our course, we’ll simply let the Venn Diagram do the work for us of showing that the existence of something in the intersection of S and P doesn’t appear to immediately imply the existence of something else which is outside of both S or P.
Summary
Here is a summary of these inferences.
| All S are P | INVALID | No S are not P | All non-P are non-S |
| No S are P | No P are S | All S are non-P | INVALID |
| Some S are P | Some P are S | Some S are not non-P | INVALID |
| Some S are not P | INVALID | Some S are non-P | Some non-P are not non-S |
For “All S are P”: CONV is INVALID; OBV produces No S are not P, and CTRA-CG produces All non-P are non-S. For “No S are P”, CONV produces No P are S, OBV produces All S are non-P, and CTRA-CG is invalid. For “Some S are P”, CONV produces “Some P are S”; OBV “Some S are not non-P”, and CTRA-CG is invalid. For Some S are not P: CONV is invalid, OBV produces “Some S are non-P”, and CTRA-CG produces “Some non-P are not non-S”.
6.2.3 Identities

Gottfried Leibniz (1646-1716), for whom “Leibniz Law” is named
The Law of Identity (=i)
Everything is identical to itself and to no other thing. The law of identity states that, for any object a, it holds true that:
a = a
Where the equality sign (=) here indicates identity. We will use lower case letters a-z to represent particular people, places, or things. These letters are called “constants”, because they represent fixed particulars. For instance, we can represent the claim that:
John = John
as:
j = j
or
George Clooney = George Clooney
as
g = g
When we want to represent that a particular object has a particular property (that it would fall into that ‘circle’ or category on a Venn Diagram), then we will write:
a is P
Where ‘a’ is whatever letter we use to stand for the object, and P is whatever letter we use to stand for the category or predicate. For instance, we’ll symbolize:
Charlie is a cat
as
c is C
where
c = Charlie
is C = “is a cat”
Notice here that we’re using the capital letter “C” to stand for the category of cats, rather than the way in which we used capital letters in the previous module, to represent whole sentences.
The law of identity entails what is called the reflexivity of identity, the property of identity where, for any x, x=x. The law of identity justifies us in writing, at any point in any argument, a statement of the form x = x, for anything in the ‘x’ spot. We cite the rule as =I, or “identity introduction”, without citing any other line in the argument:
1. c = c(=I)
The Indiscernibility of Identicals (=E)
The principle of the Indiscernibility of Identicals, also known as the rule of Identity Elimination and abbreviated “=E”, says that if two things are identical (that is, if they are not really two things but just one thing under two names), then whatever is true of the one is true of the other. More precisely, it says that for any object a, if it is true that a has property P, then for anything which is identical to a, call it b, it is true that b has property P also. In other words, the following rule of inference is valid:
1. a is P
2. b = a
3. b is P (1, 2 =E)
For instance:
1. Mark Twain is a writer.
2. Samuel Clemens is Mark Twain.
3. Samuel Clemens is a writer. (1, 2 =E)
In other words, the rule says that if a and b are identical, then we may substitute a for b, or b for a, in any proposition, without a chance in the truth value of that proposition.
Two names might be different, and people might even have different beliefs about them: people might not believe that “Samuel Clemens is the author of Huckleberry Finn” is true even though they believe that “Mark Twain is the author of Huckleberry Finn” is true. A difference in names doesn’t result in a difference in the proposition expressed, however. The same proposition is expressed by “Samuel Clemens is the author of Huckleberry Finn” and “Mark Twain is the author of Huckleberry Finn”, and if one is true then the other is true, even if these two different sentences have different significance in terms of what people think, believe, or say.
The indiscernibility of identicals is one half of a principle sometimes known as “Leibniz’s Law”, named after the philosopher and mathematician Gottfried Leibniz. Leibniz’s law also includes the converse claim, known as the identity of indiscernibles, which says that if any two things share all of the same properties, then they are identical. This is a controversial claim which belongs in a metaphysics class, however, so we’ll restrict ourselves to the indiscernibility of identicals discussed above.
Symmetry and Transitivity
We can use the rules of =I and =E to prove the symmetry and transitivity of identity.
The principle of the symmetry of identity says that, if we know that a = b, then we can conclude that b = a.
1. a = b
2. a = a (=I)
C. b = a (1, 2 =E)
The principle of the transitivity of identity says that, if we know that a = b, and we know that b = c, then we can conclude that a = c.
1. a = b
2. b = c
C. a = c (1, 2 =E)
We’ll return to these rules later in the course, but for now, they should be helpful to keep in mind as we think about categorical claims.
Application
Here is an example of how we might apply this rule within an argument:
| Symbolized | English Example |
| 1. All B are G 2. b is B 3. c = b 4. c is B (2, 3 =E) 5. c is G (1, 4 AUI) | 1. All bankers are greedy. 2. Barbara is a banker. 3. My Auntie is Barbara. 4. My Auntie is a banker. (2, 3 =E) 5. My Auntie is greedy. (1, 4 AUI) |
6.2.4 Variables

A variable can function like the arbitrary name “John Doe”.
Variables
We have already discussed using lowercase letters, like a or x or g, as constants to represent particular objects (people, things, places, etc.). Constants serve just like very short names for particular things. For instance, if h = Hermione, then h = h means “Hermione is identical to Hermione”.
There is another way in which we can use lowercase letters, however, and that is as arbitrary names or variables. Unlike constants, variables do not represent a fixed particular, but rather any arbitrary particular. We sometimes do this in English with the name “John Doe” or “Anonymous”. The detectives might not know who committed a murder, for instance, but they might refer to whoever the murder is as “John or Jane Doe”, for instance, and say “John Doe used a knife” or “Jane Doe left no fingerprints.” For instance, somebody will someday be the 100th person to read this book. Whoever the 100th person to read this book is, we might call m. We don’t know much about m, but we do know a few things. For instance, we know that m is literate, and that m somehow encountered this book.
We can use variables in logic to discuss particulars. Provided that we remember that we don’t know anything else about the particulars, there is no harm in doing so.
Existential Instantiation (EI)
The rule of existential instantiation, abbreviated (EI), says that, if we know a particular affirmative (I) or particular negative (O) claim is true, then we can use a variable or arbitrary name for the particular which falls into those categories. The rule looks like this:
- Some S are P
- x is S & x is P (1, EI)
- Some S are not P
- x is S & x is not P (1, EI)
for example:
- Some cats are homeless.
- Kittykins is a cat and Kittykins is homeless. (1, EI)
or
- Some students are not reading the textbook.
- Slacker is a student and Slacker is not reading the textbook. (1, EI)
The rule of existential instantiation might not seem very useful on its own, but it can be useful when we combine it with other rules. For instance, suppose we have these premises:
- All M are P
- Some S are M
We can now use our existing rules of &E, &I, and UI, and EG to come to a useful conclusion:
- x is S & x is M (2 EI)
- x is M (3 &E)
- x is P (2, 4 AUI)
- x is S (3 &E)
- x is S and x is P (5, 6 &I)
- Some S are P (7 EG)
This means, we can prove the following form of inference is valid:
1. All M are P
2. Some S are M
C. Some S are P
for example:
- All who are trustworthy can keep a secret.
- Some friends are trustworthy.
- Buddy is a friend and Buddy is trustworthy. (1 EI)
- Buddy is trustworthy. (3 &E)
- Buddy can keep a secret (2, 4 AUI)
- Buddy is a friend (3 &E)
- Buddy is a friend and Buddy can keep a secret. (5, 6 &I)
- Some friends can keep a secret. (7 EG)
Fallacies of Existential Instantiation
The one potential fallacy we might fall into with the rule of EI is, of course, thinking that we know something more about “Kittykins” or “Slacker” or any other arbitrary variable than we really know. So, one rule is that we must never use the same arbitrary name with the rule EI on two different sentences. For instance, the following argument is invalid:
| English | Symbolization |
| 1. Some of the applicants will get the job. 2. Hireling is an applicant and Hireling will get the job. (1, EI) 3. Some of the applicants have scary criminal records. 4. Hireling is an applicant and Hireling has a scary criminal record. (3, EI — !!INVALID!!) 5. Hireling has a scary criminal record. (4 &E) 6. Hireling will get the job. (2 &E) 7. Hireling has a scary criminal record and Hireling will get the job. (5, 6 &I) 8. Someone who has a scary criminal record will get the job. (7 EG) | 1. Some A are J 2. h is A & h is J (1, EI) 3. Some A are C 4. h is A & h is C (3, EI – !!INVALID!!) 5. h is C (4 &E) 6. h is J (2 &E) 7. h is C & h is J (5, 6 &I) 8. Some C are J (7 EG) |
The argument is invalid because on line 4, we used an arbitrary name, “Hireling”, which had already been used. A variable or arbitrary name has to be unique within the argument.
Submodule 6.2 Quiz
Licenses and Attributions
Key Sources:
- Watson, Jeffrey (2019). Introduction to Logic. Licensed under: (CC BY-SA).
Next Page: 6.3 Categorical Syllogisms
