4.4 Modeling Validity
We can model validity using truth tables when their form includes logical connectives, and using Venn Diagrams when their form involves claims about categories. In both cases we first model the premises, and then confirm that the conclusion must be true on that model.
Table of Contents
- 4.4 Modeling Validity
-
4.4.1 Validity and Truth Tables
- Step 1: Symbolize the Argument
- Step 2: One Row Per Truth Value Assignment
- Step 3: Calculate Truth Values for Premises
- Step 4: Calculate Truth Values for Conclusion
- Step 5: Highlight all Rows Where All Premises are True
- Step 6: Check if the Conclusion is true in all Highlighted Rows
- Invalid Arguments
- Extending Truth Tables
- 4.4.2 Validity and Venn Diagrams
- 4.4.3 Rules of Inference
- 4.4.4 Controversy
- Submodule 4.4 Quiz
-
4.4.1 Validity and Truth Tables
4.4.1 Validity and Truth Tables
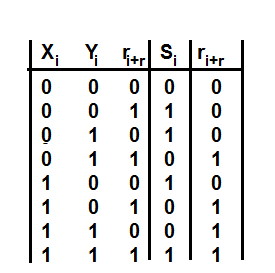
Truth tables can be used to demonstrate validity. This truth table uses ‘1’ for true and ‘0’ for false.
Step 1: Symbolize the Argument
The primary purpose of a truth table is to demonstrate that an argument or an inference is valid. We will eventually study very complex truth tables, but it will be best to start with a very simple truth table to show how the process works. Suppose that we want to show that the following argument is valid:
1. Hawaii is not a peninsula.
C. Hawaii is not not not a peninsula.
First, let’s symbolize the argument:
Let
H = “Hawaii is a peninsula”
1. ~H
C. ~~~H
Step 2: One Row Per Truth Value Assignment
The only atomic sentence right now is H. So, we start by representing each possible truth value that H might have. These possibilities are called “truth value assignments”. The first row under H represents the possibility that that H is true, and the second row under H represents the possibility that H is false.
| H | |||
| T | |||
| F |
Step 3: Calculate Truth Values for Premises
Next, we want to represent all of the possible truth values our premises might have. In this case, we have only one premise, ~H:
| H | 1. ~H | ||
| T | F | ||
| F | T |
This represents that ~H would be false if H were true, and ~H would be true if H were false.
Step 4: Calculate Truth Values for Conclusion
Next, we want to represent the possible truth values our conclusion might have. We will put the conclusion to the very right of the truth table:
| H | 1. ~H | C. ~~~H | |
| T | F | ||
| F | T |
In order to know the truth value of ~~~H, though, we first have to calculate the truth value of ~~H. So, we need to add ~~H to the truth table:
| H | 1. ~H | ~~H | C. ~~~H |
| T | F | T | |
| F | T | F |
The truth values of ~~H simply involve flipping the truth values of ~H. Now, we can calculate the truth value of ~~~H:
| H | 1. ~H | ~~H | C. ~~~H |
| T | F | T | F |
| F | T | F | T |
Hurrah! We have a completed truth table.
Step 5: Highlight all Rows Where All Premises are True
Now, how do we use this to determine whether ~~~H is a valid inference from ~H?
Well, we first want to focus only on those rows where the premises are true. We can ignore rows where the premises are false. Validity only asks if the conclusion is true in all possible worlds where the premises are true; validity is not concerned with possible worlds where the premises are false. So, we focus just on the bottom row, where ~H is T:
| H | 1. ~H | ~~H | C. ~~~H |
| T | F | T | F |
| F | T | F | T |
Step 6: Check if the Conclusion is true in all Highlighted Rows
Now, we ask whether the conclusion is true in every possible world where the premises are true. In fact, it is! The conclusion, ~~~H, has a truth value of T in row 2. So, since the conclusion is true in every row where the premises are true, the argument is valid.
Invalid Arguments
If instead the conclusion had an F in the highlighted row, the argument would have been invalid. Below is an invalid argument, and a truth table that demonstrates that it is invalid.
1. ~H
C. ~~~~H
| H | 1. ~H | ~~H | ~~~H | C. ~~~~H |
| T | F | T | F | T |
| F | T | F | T | F |
Here, the premise is true in one row, the bottom row. In this row, the conclusion is false. So, the argument has a row where the premises are true but the conclusion is false. So, the argument is invalid.
Extending Truth Tables
This is an extremely simple truth table, of course. As you might expect, when there is more than one atomic sentence (rather than just H), and more than one logical operator (rather than just ~), it gets more complicated. We will study this in later modules. For now, we hope the simple example illustrates how the process works and why.
4.4.2 Validity and Venn Diagrams

Venn Diagrams can be used to demonstrate validity.
Summary of images on this page: below are a series of Venn Diagrams, intersecting circles labelled F and G. An ‘X’ is marked in the intersection to indicate something is both F and G; an ‘X’ is marked in one but not the other to indicate something which is in one but not the other. Their intersection is shaded to indicate that no Fs are Gs; when the area in F outside of G is shaded, it indicates that nothing in F is not a G; that is, that all Fs are Gs.
Representing Categorical Claims
We can represent claims about categories of things using Venn Diagrams. Let ‘F’ and ‘G’ be categories; for instance, ‘F’ might be the category of fish (that is, all x such that “x is a fish” is true), and ‘G’ might be the category of things in the ocean (that is, all x such that “x is in the ocean” is true). We place a capital X to indicate that some things exist in that portion of the Venn Diagram, and we use shading (or scribbled lines) to indicate that nothing exists in that portion of the Venn Diagram. Here some relationships that might hold between any two categories F and G.
No information.
Some Fs are non-Gs / Some non-Gs are Fs

Some Fs are Gs / Some Gs are Fs

Some Gs are non-Fs / Some non-Fs are Gs

Some Gs are Fs / Some Gs are non-Fs
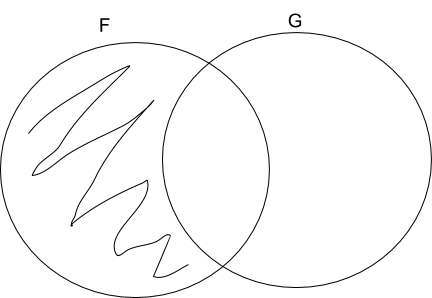
No Fs are non-Gs / All Fs are Gs / Only Gs are Fs

No Gs are Non-Fs / All Gs are Fs / Only Fs are Gs
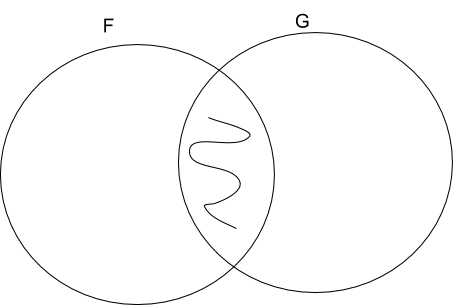
No Fs are Gs
No Gs are Fs
All Fs are Non-Gs
All Gs are Non-Fs
only non-Gs are Fs
only non-Fs are Gs
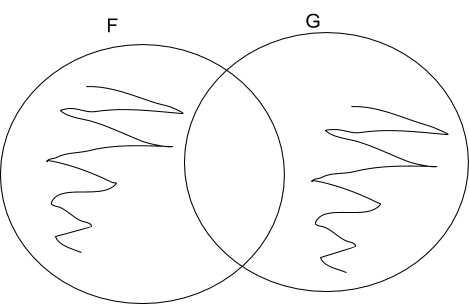
No Fs are Non-Gs
No Gs are Non-Fs
All Fs are Gs
All Gs are Fs
Only Gs are Fs
Only Fs are Gs
Testing for Validity
We can use Venn Diagrams to test the validity of an argument which involves claims about some, none, or all members of categories of things. We first draw the Venn Diagram for the premises; we then check and see whether or not the resulting venn diagram proves that the conclusion of the argument must be true.
For instance, suppose we have this argument:
1. Some fish are in the ocean
C. Not everything in the ocean is a non-fish
First, we draw the Venn Diagram for the first premise:
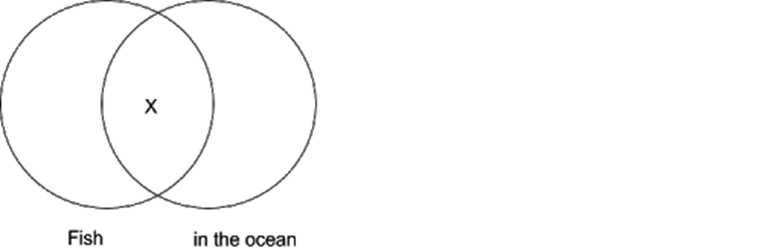
This diagram indicates that some fish are in the ocean.
Now, we look at the conclusion. Does the Venn Diagram above say that the conclusion is true, that not everything in the ocean is a non-fish? Yes, it does. To see why, imagine that instead everything in the ocean is a non-fish were true. We would then have this diagram:
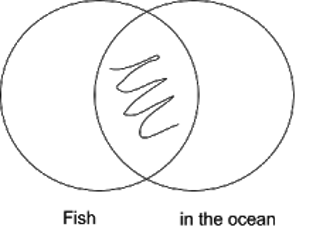
The diagram above says that no fish are in the ocean: everything in the ocean is a non-fish. But this diagram contradicts the diagram we drew earlier for premise 1, that some fish are in the ocean. An ‘X’ contradicts with shading: it can’t both be that something is in the intersection between the two categories, and that nothing is in the intersection between the two categories. So, the diagram we drew for premise one is also a diagram on which the conclusion is true. So, we’ve used a Venn Diagram to prove that the argument is valid.
4.4.3 Rules of Inference

Following rules of inference guarantees validity.
Justifying Rules of Inference
We’ve already introduced two very boring rules of inference, (DN) and (Reit.).
1. P
C. ~~P (1, DN)
1. P
C. P (1, Reit.)
Soon we will introduce some more interesting rules of inference. It is important to understand, though, how we choose rules of inference. The rules of inference we choose are not arbitrary. We don’t evaluate them based on whether they “make sense” or are intuitive, either, because some rules are not intuitive, and some inferences which “make sense” to most people are actually invalid and fallacies. Instead, we evaluate a system of rules of inference based on whether they are both sound and complete with respect to the set of logically necessary truths we want to represent.
Saying a system of rules is complete is saying that, for every conclusion which we could prove valid using a Truth Table or a Venn Diagram, there is some combination of rules we could use, going step-by-step and inference-by-inference, to derive that conclusion. Saying a system of rules is sound is saying that, for every conclusion which we arrive at step-by-step using rules of inference, the inference is actually valid, and we could prove it valid using some model like a Truth Table or Venn Diagram.
In this introductory-level class we will focus on proving the soundness of our system of rules, but not their completeness. For every rule we introduce, we will insist on using a truth table or Venn Diagram to show that every inference that can be made using the rule is always valid.
The Validity of DN
We previously proved that Reit. was valid. Now, let’s use a truth table to prove that the rule of Double Negation is valid.
Double Negation lets us add two ~~ signs, or subtract two ~~ signs, so long as we do so in pairs. So, we need to prove both cases: prove that adding two ~~ signs is always a valid inference, and prove that subtracting two ~~ is always a valid inference. Here are two truth tables, one to prove each case
Proving
1. P
C. ~~P (1, DN)
| P | 1. P | ~P | C. ~~P |
| T | T | F | T |
| F | F | T | F |
Here, we highlight the row in which Premise 1 is true. The conclusion is also true in this row. So, the argument is valid.
Proving:
1. ~~P
C. P (1, DN)
| P | ~P | 1. ~~P | C. P |
| T | F | T | T |
| F | T | F | F |
Again, we highlight the row in which Premise 1 is true. The conclusion is also true in this row. So, the argument is valid.
Truth-Functional Equivalence
We can also observe something interesting from these truth tables. Notice that P and ~~P have the same truth value on both rows. In all rows where P is T, ~~P is T, and in all rows where P is F, ~~P is F. That means that these two sentences are truth functionally equivalent.
Two sentences A and B are truth functionally equivalent if and only if they have the same truth value assignment (T or F) on every row of the truth table.
Proving a Rule is Invalid
Suppose someone proposed to us an invalid rule, like “single negation”. They claim the following inference is valid:
- P
- ~P (1, Single Negation)
How would we prove them wrong? Well, we simply create a truth table with the premise and the conclusion, and we highlight the rows where the premise is true.
| P | 1. P | C. ~P |
| T | T | F |
| F | F | T |
There is a highlighted row where the premise is true, but the conclusion is false. If there is at least one highlighted row where the premise is true but the conclusion is false, then the argument is invalid. So, the rule we used, “single negation” is also invalid.
4.4.4 Controversy

Abstracting away from the particulars of a debate can help defuse controversy.
Controversy and Abstraction
In this module, we’ve looked at some of the tools of formal logic: symbolization, truth tables, Venn Diagrams, and rules of inference, and we’ve seen some basic examples of how each of them works. We will spend the next several modules expanding what we can do with these formal tools and handling more complex arguments. As the course becomes more abstract, students often wonder what the purpose is of all of this abstraction.
There are many reasons someone might want to study formal logic: for some people, logic games are just kind of fun. One main reason it is valuable to develop abstract thinking, however, is to help us think more clearly about issues when there is significant controversy and disagreement. Although we can apply symbolization, truth tables, Venn Diagrams, and rules of inference to any sort of argument or inference, including silly topics, the point of learning this system is to be able to more objectively handle real controversies. Formal tools allow us to take a step back from the emotion and the controversy to study the form of an argument, and to see whether the conclusion really follows from the premises, or whether any inferences in the argument are invalid. Keep this in mind as we study tools to model validity: there is a point to all of this, and that’s to allow us to think through controversial topics together.
Submodule 4.4 Quiz
Licenses and Attributions
Key Sources:
- Watson, Jeffrey (2019). Introduction to Logic. Licensed under: (CC BY-SA).
