4.1 The Form of an Argument

Symbolizing claims helps us focus on the form of an argument rather than its content. We begin by symbolizing simple statements and negations of simple statements. The negation of a simple statement is false whenever the simple statement is true, and it is false whenever the simple statement is true.

Table of Contents

• 4.1 The Form of an Argument
  • 4.1.1 Introduction to Formal Logic
    • Formal Logic
    • Symbolizing
    • Rules of Inference
  • 4.1.2 What to Symbolize
    • Symbolize Statements
    • Single, Complete Sentences
    • Breaking Up Sentences
  • 4.1.3 Symbolization: Positive Claims
    • Writing a Dictionary
    • Simple Statements
    • The Rule of Reiteration (Reit.)
    • Proving the Validity of Reiteration (Reit.)
  • 4.1.4 Symbolization: Negative Claims
    • Negation
    • Symbolizing Negation
  • Submodule 4.1 Quiz

4.1.1 Introduction to Formal Logic

George Boole (1815-1864) was an important developer of modern logic.

Formal Logic

We have defined a formal argument as:

a numbered list of premises, followed by intermediate steps or inferences that follow from those premises, followed by a conclusion.

We have defined a valid argument as one for which:

there is no possibility of the premises being true with the conclusion being false.

Being a valid argument is not the same as being a good argument. Validity has to do with the form or structure of the argument rather than the content of the argument. It means that, given the structure of the argument, there is no logical possibility of true premises with a false conclusion. We have seen many examples of invalid arguments and fallacious inferences. Now we are ready to begin to study which forms of argument are guaranteed to be valid. This study is called formal logic.

Over the next few modules, you will learn how to use four tools from formal logic: Venn Diagrams, Symbolization, Rules of Inference, and Truth tables. We’ll begin with extremely simple cases, but they will become complicated quickly!

Symbolizing

Symbolizing sentences helps us ignore the content and focus on the form of the sentence, and that helps us to recognize the form of an argument made up of those sentences. Our tendency is to focus on the content of an argument first, but we can improve the inferences we make by first studying the form of an argument. For example, the three sentences below have very different content:

The dog is not at home and the cat is asleep.

The nuclear weapons aren’t deployed but the Navy is under attack.

Laura isn’t in love with Daniel and it’s time for Daniel to move on.

Nonetheless, all three sentences have the very same logical form:

NOT-P AND Q

Truth Tables

Truth tables are a way of coming up with a complete list of all of the possible scenarios, in order to determine whether there is no possible world where the premises are true with the conclusion false; that is, whether an argument is valid or invalid. Each row on the truth table is called a truth value assignment and it represents a type of “possible world”. Below are the four possible combinations of “True” (represented by T) and “False” (represented by F) truth values for the propositions P and Q:

P	Q
True	True
True	False
False	True
False	False

Rules of Inference

Rules of Inference are fixed patterns that an argument or inference can follow which are always valid. For instance, the pattern below, known as modus ponens, is always valid:

1. IF Y THEN Z

2. Y

C. Z (1,2)

For instance:

1. If you drank coffee, then you have energy.

2. You drank coffee.

C. You have energy. (1, 2 Modus Ponens)

Venn Diagrams
Lastly, we will learn how to use Venn Diagrams to determine whether or not an inference is valid. In the way Logic uses Venn Diagrams, the circles represent general categories of things. The lines or shaded space indicate that nothing is in that section of the Venn Diagram, it is a kind of “black hole”; the blank or unshaded space indicates that something might be in that section of the Venn Diagram. 

The diagram below represents that: 

No As are not Bs 

It also represents that: 

All As are Bs 

The Venn Diagram can help show that these two claims are logically equivalent, no matter what “A” and “B” are. For instance, we can see using the Venn Diagram that “No politicians are not liars” is logically equivalent to “All politicians are liars.”

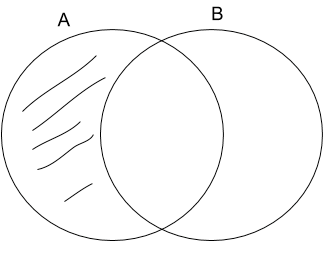
The shaded area represents that nothing is in that area.

---

4.1.2 What to Symbolize

Declarative sentences make claims about the world.

Symbolize Statements

Remember that propositions are claims about the world which are capable of being true or false about the world. If you say something which can’t be either true or false, then you’re not really making a claim. For example, if you say “Go home!”, you’re not making a claim. Claims can be about the way things actually are, like “Phoenix has a light rail system”, or about the way they were or will be, like “Phoenix will soon have a longer light rail system”, or about the way things could, would, or might be, like “Phoenix might have never built a light rail system.” Claims can also be about the way things ought to be or should be, like “Phoenix should have a better light rail system.”

The premises and conclusion of a formal argument must express propositions. They must be statements (declarative sentences). The premises and conclusion must not be interrogative sentences (questions), exclamatory sentences (expressions of feeling), or imperative sentences (commands or requests). The following is not an argument:

1. You loser!
2. Get lost!
3. Booooooooooooo!

C. Why are you still here?

The following is an argument:

1. You are a loser.
2. You should get lost.
3. If you are a loser and you should get lost, then you should not still be here.

C. You should not still be here.

Single, Complete Sentences

The sentences in a formal argument must also be single, complete sentences. Multiple sentences are not allowed as premises or conclusions. This is not permitted:

C. We should regulate firearms. We should not allow violence to continue. We are better than this.

Likewise, incomplete sentences are not allowed as premises or conclusions. The following is not an argument:

1. The economic data
2. What my information sources say

C. Time to sell bonds.

For the purposes of our class, only single, complete, declarative sentences can be symbolized.

Breaking Up Sentences

Lastly, when symbolizing it is better not to attempt to symbolize sentences which contain arguments or inferences within themselves. Because our goal is to represent arguments or inferences, if a sentence contains an argument within itself, we will miss out on symbolizing the actual inference. For example, these sentences contain inferences within themselves, marked by the words “since”, “because”, and “so that”:

1. Since you admire Ali, Ali will let you hang out with her.
2. Calli is jealous because Ali will let you hang out with her.

Instead, in order to prepare to symbolize these sentences, we need to first break them into smaller pieces, and use standardized language (“if-then”), so that the inferences are clear. For instance:

1. You admire Ali.
2. If you admire Ali, then Ali will let you hang out with her.
3. Ali will let you hang out with her.

---

4.1.3 Symbolization: Positive Claims

Capital letters represent whole sentences.

Writing a Dictionary

The first step in symbolizing claims is composing a “dictionary”; not a dictionary like Merriam Webster’s, but a way of translating between symbols and the statements which those symbols represent. The symbols conventionally used for simple statements are capital letters (A, B, C . . . X, Y, Z, etc.). Any capital letter can be used to represent any sentence: although as a memory device it’s typical to use a letter with which one of the memorable words in the sentence begins, it isn’t a requirement to do so. In the rare case that one runs out of capital letters, subscripts may be used: (N1, D2, G62, etc.). A dictionary looks like this:

Let:

A = “Armadillos attacked Atlanta.”

D = “Elaine questioned the sincerity of the proposal.”

Z = “The children want to play with zirconium.

Simple Statements

The sentences which we symbolize with single letters are called atomic sentences or “simple statements”. These sentences are positive rather than negative in the sense that they don’t contain words like “no”, “not”, “isn’t”, “don’t”, “it is not the case that”, “neither”, or “none”. Notice that all of the simple statements above are single, complete sentences which express a proposition and which do not contain arguments embedded within themselves. They are also missing words which indicate logical complexity like “or”, “and”, “if”, and “then”, which we will learn to symbolize later. So, from the perspective of propositional logic, they have the same logical form, despite having very different content. A dictionary should contain a translation for every atomic sentence used in an argument.

The Rule of Reiteration (Reit.)

There is only one rule of inference which applies to simple statements by themselves, although it is a painfully obvious rule. This rule says that you may infer anything from itself. It is called the rule of reiteration. For instance, if you know that it is Tuesday, then you can infer from this that it is Tuesday.

Let T = “It is Tuesday”.

1. T
2. T (1, Reit.)

Notice that we write (1, Reit.) on line 2 to indicate that “T” on line 2 is inferred from “T” on line 1 through the use of the rule of reiteration (abbreviated Reit.) All rules of inference will have this structure: we’ll cite the lines the inference was derived from, followed by a comma, followed by the rule used to derive it.

Proving the Validity of Reiteration (Reit.)

We can prove that the rule of reiteration is valid by constructing a truth table:

1. T	2. T
True	True
False	False

There are two possible truth values which T on line 1 might have: it could be true, or it could be false. The left column represents these two possibilities: the first row represents the possibility where line 1 is true, and the second row represents the possibility where line 1 is false. Since line 2 also has the letter T, which is the same proposition, the right column of the truth table matches the left column. 

To determine whether this inference is valid, we ask whether there is a counterexample to validity. A counterexample would be a “possible world” (a row) where line 1 is true but line 2 is false. In row 1, line 1 is true and line 2 is true, so row 1 is not a counterexample. In row 2, line 1 is false, so row 2 is not a counterexample. Since neither is a counterexample, the inference, and the rule of Reiteration we used to derive it, is valid.

---

4.1.4 Symbolization: Negative Claims

The Tilde (~) is the negation sign, which ‘flips’ True to False, and False to True

Negation

The sentence “Natasha wants an apple” and the sentence “Natasha does not want an apple” will always have different truth values. If it is true that “Natasha wants an apple”, then it is false that “Natasha does not want an apple.” If it is false that “Natasha wants an apple” then it is true that “Natasha does not want an apple.”

“Natasha does not want an apple” is called the negation of “Natasha wants an apple.” The negation of a simple statement is the statement which we get by adding the word not, to the statement, or it is not the case that in front of the statement. The negation of a simple statement will be true whenever the statement is false, and false whenever it is true.

The negation of a statement is not the same as the opposite of a statement. The negation of the statement, “Jeff loves peaches” is “Jeff does not love peaches”. The opposite of the statement, “Jeff loves peaches” is “Jeff hates peaches”. But Jeff might not hate peaches, and yet also not love them. So “Jeff hates peaches” is not the negation of “Jeff loves peaches.”

Any adverbs which modify in a statement also appear in its negation. For instance, the negation of “Jeff ran quickly” is not “Jeff did not run”, but rather “Jeff did not run quickly.” It might be that Jeff ran, but not quickly.

Symbolizing Negation

We will use a tilde ~ sign to symbolize negation. Some other logic textbooks use the ¬ sign, which is the same thing. We won’t use the negation sign from mathematics (−), though, because that would confuse things: negated sentences do not behave like negative numbers. To symbolize a negative sentence, we first symbolize the positive simple sentence using a capital letter, and then we place the tilde before the letter. For instance suppose we want to symbolize:

“That was not the most amazing burger I have ever eaten.”

First, we create this dictionary: 

Let:

B = “That was the most amazing burger I have ever eaten.”

Then we symbolize: 

~B = “That was not the most amazing burger I have ever eaten.” 

Here are some more examples: 

Let:

C = “Chocolate cows melt in the sun.” 

Then: 

~C = “Chocolate cows don’t melt in the sun.” 

Let:

H = “Harriet is already retired.”

Then:

~H = “Harriet isn’t already retired.”

Let:

T = “The golden sun sways in the sky.

Then:

~T = “It isn’t the case that the golden sun sways in the sky.” 

---

Submodule 4.1 Quiz

Licenses and Attributions

Key Sources:

• Watson, Jeffrey (2019). Introduction to Logic. Licensed under: (CC BY-SA).

Next Page: 4.2 True and False