6.3 Categorical Syllogisms

This module presents the rules for valid categorical syllogisms, and the fifteen valid forms of categorical syllogism. We begin with three clearly valid forms, then present the six rules and the fallacies which violate the six rules. We then show how to categorize categorical syllogisms by mood and figure, and then present the 15 valid mood/figure combinations. Only these 15 forms of categorical syllogism are valid.

Table of Contents

• 6.3 Categorical Syllogisms
  • 6.3.1 Three Valid Forms of Categorical Syllogism
    • Three Valid Forms of Categorical Syllogism (CS)
    • The Form of a Categorical Syllogism
    • What Categorical Syllogisms are Valid?
  • 6.3.2 Fallacies and Categorical Syllogisms
    • Fallacies of Categorical Syllogism
    • The Fallacy of Four Terms
    • Undistributed Middle
    • Illicit Major or Minor
      • Illicit Minor
      • Illicit Major
    • Exclusive Premises
    • Affirmative from Negative
    • Existential Fallacy
  • 6.3.3 Mood and Figure for Categorical Syllogism
    • Standard Form
    • Mood
    • Figure
    • Here is a summary of the four figures
  • 6.3.4 Valid Categorical Syllogisms of the First Figure
    • First Figure
  • 6.3.5 Valid Categorical Syllogisms of the Second Figure
    • Second Figure
  • 6.3.6 Valid Categorical Syllogisms of the Third Figure
    • Third Figure
  • 6.3.7 Valid Categorical Syllogisms of the Fourth Figure
    • Fourth Figure
  • Submodule 6.3 Quiz

6.3.1 Three Valid Forms of Categorical Syllogism

All humans are mortal. All logic students are human. Therefore, all logic students are mortal.

Three Valid Forms of Categorical Syllogism (CS)

In the previous sub-module, we demonstrated that three inferences were valid using the rule of Existential Instantiation, as well as other rules for Universals and Existentials. These inferences, as well as some others which we will study in this sub-module, share in common a form which we call Categorical Syllogism. When we prove that an inference is valid using other rules we know to be valid, we can add that valid form of inference to our set of valid rules. So we’ll add these inferences to our set of rules, abbreviating them (CS), for “Categorical Syllogism”.

1. Some M are not P
2. All M are S
3. Some S are not P (1, 2 CS)

1. All M are P
2. Some M are S
3. Some S are P (1, 2 CS)

1. All M are P
2. Some S are M
3. Some S are P (1, 2 CS)

The Form of a Categorical Syllogism

What form do these inferences all have in common? A categorical syllogism is an argument consisting of exactly three categorical propositions (two premises and a conclusion) in which there appear a total of exactly three categorical terms, each of which is used exactly twice.

One of those terms must be used as the “subject term” of the conclusion of the syllogism, and we call it the “minor term” of the syllogism as a whole:

1. S are P

The “major term” of the syllogism is whatever is employed as the predicate term of its conclusion:

1. S are P

The third term in the syllogism doesn’t occur in the conclusion at all, but must be employed in somewhere in each of its premises. We call it the middle term:

1. S are M
2. M are P
3. S are P

Since one of the premises of the syllogism must be a categorical proposition that affirms some relation between its middle and major terms, we call that the major premise of the syllogism. The other premise, which links the middle and minor terms, we call the minor premise.

Consider, for example, the categorical syllogism:

1. No geese are felines.
2. Some birds are geese.
3. Some birds are not felines.

Clearly, “Some birds are not felines” is the conclusion of this syllogism. The major term of the syllogism is “felines” (the predicate term of its conclusion), so “No geese are felines” (the premise in which “felines” appears) is its major premise. Similarly, the minor term of the syllogism is “birds,” and “Some birds are geese” is its minor premise. “Geese” is the middle term of the syllogism:

1. No M are P
2. Some S are M
3. Some S are P

What Categorical Syllogisms are Valid?

Since the validity of a categorical syllogism depends solely upon its logical form, it is relatively simple to state the conditions under which the premises of syllogisms succeed in guaranteeing the truth of their conclusions. Relying heavily upon the medieval tradition, the logicians Copi & Cohen provide a list of six rules, each of which states a necessary condition for the validity of any categorical syllogism. Violating any of these rules involves committing one of the formal fallacies, errors in reasoning that result from reliance on an invalid logical form.

In every valid standard-form categorical syllogism . . .

1. . . . there must be exactly three unambiguous categorical terms.
2. . . . the middle term must be distributed in at least one premise.
3. . . . any term distributed in the conclusion must also be distributed in its premise.
4. . . . at least one premise must be affirmative.
5. . . . if either premise is negative, the conclusion must also be negative.
6. . . . if both premises are universal, then the conclusion must also be universal.

“Distributed” means that the premises provide information about the whole category into which the term falls, rather than just particular members of the term. In practice, this means that the term either:

1. Appears in the subject of a universal affirmative (All S are P)
2. Appears in the predicate of a particular negative (Some S are not P)
3. Appears in the subject or predicate of a universal negative (No S are P)

Although it is possible to identify additional features shared by all valid categorical syllogisms (none of them, for example, have two particular premises), these six rules are jointly sufficient to distinguish between valid and invalid syllogisms.

---

6.3.2 Fallacies and Categorical Syllogisms

The Six Fallacies of Categorical Syllogism are for fools.

[Content on this page from http://www.philosophypages.com/lg/e08b.htm and http://www.philosophypages.com/dy/f9.htm , The Philosophy Pages by Garth Kemerling are licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.]

Fallacies of Categorical Syllogism

Remember that any violation of our six rules for categorical syllogism results in a fallacy:

1. . . . there must be exactly three unambiguous categorical terms:
2. . . . the middle term must be distributed in at least one premise.
3. . . . any term distributed in the conclusion must also be distributed in its premise.
4. . . . at least one premise must be affirmative.
5. . . . if either premise is negative, the conclusion must also be negative.
6. . . . if both premises are universal, then the conclusion must also be universal.

Remember that “Distributed” means that the premises provide information about the whole category into which the term falls, rather than just particular members of the term, i.e., it:

1. Appears in the subject of a universal affirmative (All S are P)
2. Appears in the predicate of a particular negative (Some S are not P)
3. Appears in the subject or predicate of a universal negative (No S are P)

Let’s look at the six fallacies for categorical syllogisms.

The Fallacy of Four Terms

The Fallacy of Four Terms violates the first rule, that there must be exactly three unambiguous categorical terms. It employs more than three distinct categorical terms:

1. All M are P
2. All S are A
3. All S are P !!INVALID!!

Example: “All managers are politicians, and all sybarites are administrators, so all sybarites are politicians.”

Undistributed Middle

The Fallacy of Undistributed Middle violates the second rule, that the middle term must be distributed in at least one premise.

1. All S are M
2. Some M are P
3. Some S are P !!INVALID!!

M is not “distributed” because it occurs only in the predicate of a universal affirmative (1), and in a particular affirmative (2), so we have no information about the whole class of M.

Example: All dogs are mammals. Some mammals are whales. Therefore, some dogs are whales.

Illicit Major or Minor

The fallacies of illicit major or minor violate the third rule, that any term distributed in the conclusion must also be distributed in its premise.

Illicit Minor

1. All M are P
2. All M are S
3. All S are P

Here, S is distributed in the conclusion (3), but not in either premise.

Example: All poodles are mammals. All poodles are pets. Therefore, All pets are mammals.

Illicit Major

1. All M are P
2. No S are M
3. No S are P

Here, P is distributed in the conclusion, but not in either premise.

Example: All dogs are mammals. No cats are dogs. Therefore, no cats are mammals.

Exclusive Premises

The Fallacy of Exclusive Premises violates the fourth rule. It is invalid because  because both of its premises are negative.

1. No P are M
2. Some M are not S
3. Some S are not P

Example: Since no mammals are fish and some fish are not whales, it follows that some whales are not mammals.

Affirmative from Negative

The Fallacy Concluding an Affirmative from a Negative violates the fifth rule, by having an affirmative conclusion derived from at least one negative proposition as a premise.

1.  All M are P
2. No S are M
3. All S are P

Example: “All senators are eligible to vote on legislation, but no homeless people are senators, so all homeless people are eligible to vote on legislation.”

The problem with any such reasoning is that the exclusion of one class from another cannot provide deductively certain grounds for the inclusion of either of these classes with another.

Existential Fallacy

The Existential Fallacy violates the sixth rule. It is invalid because it has two universal premises and a particular conclusion.

1. All M are P
2. All S are M
3. Some S are P

Example: “All inhabitants of another planet are friendly people, and all Martians are inhabitants of another planet. Therefore, some Martians are friendly people.”

---

6.3.3 Mood and Figure for Categorical Syllogism

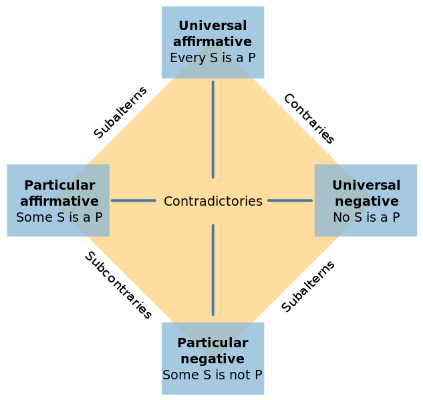
The Square of Opposition. Particular Affirmatives (Some S is a P) are contradictory with Universal Negatives (No S is a P). Universal affirmatives (Every S is a P) are contradictory to Particular negatives (Some S is not P). The relations of  contraries, subalterns and subcontraries are listed, which hold only on the assumption that some S exists. Assuming an S exists, universal affirmative or negative propositions imply their subalterns in particular affirmative or negative propositions; assuming an S exists, particular affirmatives and particular negatives are ‘subcontraries’, meaning both cannot be false. Assuming an S exists, Universal Negatives and Universal Affirmatives are contraries, since they cannot both be true).

[Content modified from http://www.philosophypages.com/lg/e08a.htm, The Philosophy Pages by Garth Kemerling. Licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.]

Standard Form

In order to make obvious the similarities of structure shared by different syllogisms, we will always present each of them in the same fashion. A categorical syllogism in standard form always begins with the premises, the first premise consisting of a middle term and the predicate of the conclusion, the second premise consisting of a middle term and the subject of the conclusion, and then finishes with the conclusion itself. 

Although arguments in ordinary language may be offered in a different arrangement, it is never difficult to restate them in standard form. For example:

I know that some politicians are corrupt individuals, because everybody who accepts campaign contributions is a politician, and some people who accept campaign contributions are corrupt individuals.

We start by identifying the conclusion, which is underlined above. Then we note subject and predicate of the conclusion:

C. Some politicians are corrupt individuals

“Politicians” is the subject, and “corrupt individuals” is the predicate.

The middle term is “person who accepts campaign contributions”. That’s because it is the term which occurs in the premises but not the conclusion.

Once we’ve identified the conclusion which is to be placed in the final position, whichever premise contains its predicate term must be the first premise. 

Since “corrupt individuals” is the predicate of the conclusion, the first premise must contain it. So the first premise must be:

1. Some people who accept campaign contributions are corrupt individuals.

The second premise contains the subject of the conclusion, “politicians”:

2. Everybody who accepts campaign contributions is a politician.

So, in standard form, we have:

1. Some people who accept campaign contributions are corrupt individuals.

2. Everybody who accepts campaign contributions is a politician.

C. Some politicians are corrupt individuals

Once we have the argument in standard form, we can determine its mood and figure.

Mood

Recall our four sentences types from earlier: 

A: All S are P 
E: No S are P 
I: Some S are P 
O: Some S are not P

Medieval logicians devised a simple way of labelling the various forms in which a categorical syllogism may occur by stating its mood and figure. The mood of a syllogism is simply a statement of which categorical propositions (A, E, I, or O) it is comprised of, listed in the order in which they appear in standard form. 

Thus, a syllogism with a mood of OAO has an O proposition as its major premise, an A proposition as its minor premise, and another O proposition as its conclusion; and EIO syllogism has an E major premise, an I minor premise, and an O conclusion. 

More examples: 

MOOD = OAO 

1. Some M are not P   =   O

2. All M are S   =   A 
C. Some S are not P (1, 2 CS)   =   O 

MOOD = AII

1. All M are P   =   A
2. Some M are S   =   I 
C. Some S are P (1, 2 CS)   =   I

MOOD = AII

1. All M are P   =   A 
2. Some S are M   =   I
C. Some S are P (1, 2 CS)   =   I 

Looking at our earlier example, we have:

 1. Some people who accept campaign contributions are corrupt individuals. (Some M are S)

 2. Everybody who accepts campaign contributions is a politician.  (All M are S)

 C. Some politicians are corrupt individuals (Some S are P)

This has the mood

1. Some M are P = I

2. All M are S = A

C. Some S are P = I 

Figure

Mood alone is not enough to categorize all of the forms of categorical syllogism. We need to supplement this labelling system with a statement of the figure of each, which is solely determined by the position in which its middle term appears in the two premises: in a first-figure syllogism, the middle term is the subject term of the major premise and the predicate term of the minor premise; in second figure, the middle term is the predicate term of both premises; in third, the subject term of both premises; and in fourth figure, the middle term appears as the predicate term of the major premise and the subject term of the minor premise. The four figures may be easier to remember as a simple chart showing the position of the terms in each of the premises.  

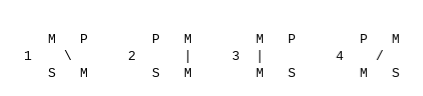
 Looking at our earlier example, we have: 

 1. Some people who accept campaign contributions are corrupt individuals. (Some M are S) 

 2. Everybody who accepts campaign contributions is a politician. (All M are S) 

 C. Some politicians are corrupt individuals (Some S are P) 

Earlier we noted this was of mood IAI.  This has the figure: 

1. Some M are P

2. All M are S

C. Some S are P

Since the middle terms M are both on the left hand side, it is of figure three. So its mood and figure is IAI-3

This method of differentiating syllogisms is significant because the validity of a categorical syllogism depends solely upon its logical form. An argument is valid when, if its premises were true, then its conclusion would also have to be true. The content is irrelevant: it makes no difference whether the categorical terms it employs are “mammals,” “terriers,” and “dogs” or “sheep,” “commuters,” and “sandwiches.” What matters is the form, not the content. 

Even though there are 256 possible forms of Categorical Syllogism, only 15 forms are valid. So it is important to recognize mood and figure in order to know whether or not a Categorical Syllogism is valid.

We’ll look closely at the 15 valid moods and figures on the following pages. They are:

AAA-1

EAE-1 EAE-2

AII-1  AII-3 

EIO-1 EIO-2 EIO-3 EIO-4 

AEE-2 AEE-4

OAO-3  

AOO-2

IAI-3 IAI-4

Here is a summary of the four figures

First figure (middle term is diagonal \ from upper left to lower right) 

1. M are P 

2. S are M 

C. S are P 

Second figure (middle terms on the right |) 

1. P are M 

2. S are M 

C. S are P 

Third figure (middle terms on the left |)

1. M are P 

2. M are S 

C. S are P 

Fourth figure (middle term is diagonal / from upper right to lower left)

1. P are M 

2. M are S 

C. S are P 

Used together, mood and figure provide a unique way of describing the logical structure of each of them. 

---

6.3.4 Valid Categorical Syllogisms of the First Figure

Below are Venn Diagrams with three intersecting circles, labelled ‘S’, ‘P’, and ‘M’, indicating the valid categorical syllogisms of the first figure. 

[Image Credit: REPRESENTACIÓN GRÁFICA DE LOS MODOS VALIDOS DE SILOGISMO EN DIAGRAMAS DE VENN by MONIMINO]

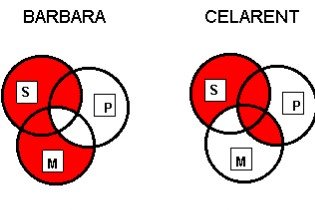
Modus Barbara: All areas of M and S are shaded except where M intersects with P. Modus Celarent: All areas of P are shaded where it intersects with other circles, and all areas of S except where it intersects with M but not with P.

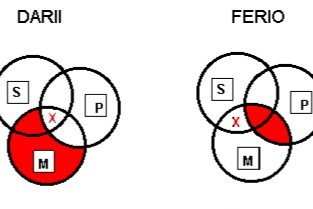
Modus Darii: all areas of M are shaded except where it intersects with P; an X is in the intersection of all three circles. Modus Ferio: the intersection of M and P is shaded, and there is an X where S and M intersect with one another but not with P.

[Content from http://www.philosophypages.com/lg/e08a.htm and http://www.philosophypages.com/dy/f9.htm#fres , The Philosophy Pages by Garth Kemerling are licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.]

First Figure

We noted earlier, that even though there are 256 forms of Categorical Syllogism, only 15 of those forms are valid arguments. We’ll study those 15 forms of argument in terms of their figure. Recall that these are the four figures:

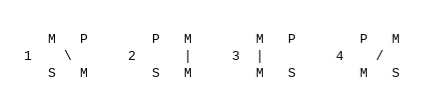
We’ll start with the first figure, where the structure of the argument looks like this:

1. M are P
2. S are M
C. S are P

There are four valid forms of Categorical Syllogism for the first figure. We’ll present them by first giving their Mood (AEI, OEO, etc.), then giving their figure, and then giving their traditional Medieval name (created to match their mood). We’ll then present the valid form, followed by an example.

AAA-1: “Barbara”

1. All M are P.
2. All S are M.
C. All S are P.

Example: All finches are birds, and all cardinals are finches, so all cardinals are birds.

Instances of this form are especially powerful, since they are the only valid syllogisms whose conclusions are universal affirmative propositions.

EAE-1: “Celarent”

1. No M are P.
2. All S are M.
c. No S are P.

Example: No cold-blooded animals are furry pets, even though all reptiles are cold-blooded animals; therefore, no reptiles are furry pets.

AII-1: “Darii”

1. All M are P.
2. Some S are M.
C. Some S are P.

Example: All logicians are philosophers, and some serious scholars are logicians, so some serious scholars are philosophers.

EIO-1: “Ferio”

1. No M are P.
2. Some S are M.
C. Some S are not P.

Example: No mendicant friars are wealthy patrons of the arts, but some medieval philosophers are mendicant friars, so some medieval philosophers are not wealthy patrons of the arts.

6.3.5 Valid Categorical Syllogisms of the Second Figure

Below are Venn Diagrams with three intersecting circles, labelled ‘S’, ‘P’, and ‘M’, indicating the valid categorical syllogisms of the second figure. 

[Image Credit: REPRESENTACIÓN GRÁFICA DE LOS MODOS VALIDOS DE SILOGISMO EN DIAGRAMAS DE VENN by MONIMINO]

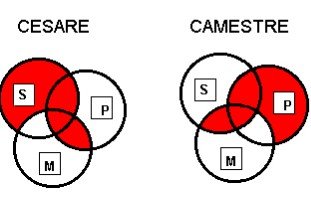
Modus Cesare: All of S is shaded except where it intersets with M but not P; all of P is shaded where it intersects with another circle. Modus Camestre: All of P is shaded except where it intersects with M but not S; all of S is shaded where it intersets with another circle.

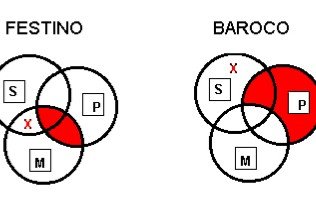
Modus Festino: the intersection of P and M is shaded; there is an X where S and M intersect but not P.  Modus Baroco: there is an X in S which is outside of P or M; all of P is shaded except where it intersects with M.

[Content from http://www.philosophypages.com/lg/e08a.htm and http://www.philosophypages.com/dy/f9.htm#fres , The Philosophy Pages by Garth Kemerling are licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.]

Second Figure

We’ll turn now to the second figure, where the structure of the argument looks like this:

1. P are M
2. S are M
C. S are P

There are also four valid forms of Categorical Syllogism for the second figure. We’ll again present them by first giving their Mood (AEI, OEO, etc.), then giving their figure, and then giving their traditional Medieval name (created to match their mood), and then the valid form, followed by an example.

EIO-2: “Festino”

1. No P are M
2. Some S are M.
C. Some S are not P

Example: No people deserving of our admiration and praise are inveterate liars, but some wealthy industrialists are inveterate liars; therefore, some wealthy industrialists are not people deserving of our admiration and praise.

EAE-2: “Cesare”

1. No P are M
2. All S are M.
C. No S are P

Example: Since no truly peaceful nations are places where basic human rights are inadequately defended, while all countries torn by ethnic strife are places where basic human rights are inadequately defended, it follows that no countries torn by ethnic strife are truly peaceful nations.

AEE-2: “Camestres”

1. All P are M
2. No S are M.
C. No S are P

Example: All terriers are dogs, while no cats are dogs, so no cats are terriers.

AOO-2: “Baroco”

1. All P are M
2. Some S are not M
C. Some S are not P

Example: All cats are furry mammals, but some house pets are not furry mammals, so some house pets are not cats.

6.3.6 Valid Categorical Syllogisms of the Third Figure

Below are Venn Diagrams with three intersecting circles, labelled ‘S’, ‘P’, and ‘M’, indicating the valid categorical syllogisms of the third figure. 

[Image Credit: REPRESENTACIÓN GRÁFICA DE LOS MODOS VALIDOS DE SILOGISMO EN DIAGRAMAS DE VENN by MONIMINO]

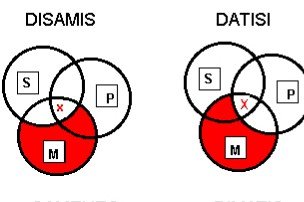
Modus Disamis: All of M is shaded except where it intersects with S; there is an X where all three circles intersect; Modus Datisi: All of M is shaded except where it intersects with P; there is an X where all three circles intersect.

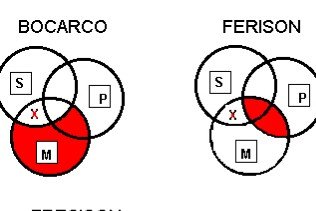
Modus Bocarco: All of M is shaded except where it intersects with S; there is an X where S and M intersect but not P; Modus Ferison: there is an X where S and M intersect but not P, and shading where M and P intersect.

[Content from http://www.philosophypages.com/lg/e08a.htm and http://www.philosophypages.com/dy/f9.htm#fres , The Philosophy Pages by Garth Kemerling are licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.]

Third Figure

We’ll turn now to the third figure, where the structure of the argument looks like this:

1. M are P
2. M are S
C. S are P

Just as the first and second figure, there are also four valid forms of Categorical Syllogism for the third figure. We’ll once again present them by first giving their Mood (AEI, OEO, etc.), then giving their figure, and then giving their traditional Medieval name (created to match their mood), and then the valid form, followed by an example.

OAO-3: “Bocardo”

1. Some M are not P
2. All M are S
C. Some S are not P

Example: Some local jails are not maximum-security prisons, but since all local jails are correctional institutions, it follows that some correctional institutions are not maximum-security prisons.

AII-3: “Datisi”

1, All M are P
2. Some M are S
C. Some S are P

Example: Since all bookstores are places that sell popular novels and some bookstores are coffee shops, it follows that some coffee shops are places that sell popular novels.

IAI-3: “Disamis”

1. Some M are P
2. All M are S
C. Some S are P

Example: Some nutritious dinners are vegetarian delights, and all nutritious dinners are well-rounded meals, so some well-rounded meals are vegetarian delights.

EIO-3: “Ferison”

1. No M are P
2. Some M are S
C. Some S are not P

Example: Since no people who admire Marx are political conservatives and some people who admire Marx are South Carolinians, it follows that some South Carolinians are not political conservatives.

---

6.3.7 Valid Categorical Syllogisms of the Fourth Figure

Below are Venn Diagrams with three intersecting circles, labelled ‘S’, ‘P’, and ‘M’, indicating the valid categorical syllogisms of the fourth figure. 

[Image Credit: REPRESENTACIÓN GRÁFICA DE LOS MODOS VALIDOS DE SILOGISMO EN DIAGRAMAS DE VENN by MONIMINO]

Modus Camenes: all of P is shaded except where it intersects with M; all of S is shaded where it intersects with other circles. Dimatis: All of M is shaded except where it intersects with S; there is an x where all three circles intersect.

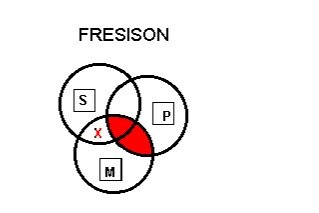
Modus Fresison: the intersetion of M and P is shaded, and there is an X where M and S intersect outside of P.

[Content from http://www.philosophypages.com/lg/e08a.htm and http://www.philosophypages.com/dy/f9.htm#fres , The Philosophy Pages by Garth Kemerling are licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.]

Fourth Figure

We’ll turn now to the fourth figure, where the structure of the argument looks like this:

1. P are M
2. M are S
C. S are P

Unlike the other figures, there are only three valid forms of Categorical Syllogism for the fourth figure. We’ll once again present them by first giving their Mood (AEI, OEO, etc.), then giving their figure, and then giving their traditional Medieval name (created to match their mood), and then the valid form, followed by an example.

EIO-4: “Fresison”

1. No P are M
2. Some M are S
C. Some S are not P

Example: Since no fish are mammals while some animals that live in water are mammals, it follows that some animals that live in water are not fish.

IAI-4: “Dimatis” or “Dimaris”

1. Some P are M
2. All M are S
C. Some S are P

Example: Some beloved household pets are golden retrievers, and since all golden retrievers are dogs, it must follow that some dogs are beloved household pets.

AEE-4: “Calemes” or “Camenes”

1. All P are M
2. No M are S
C. No S are P

Example: All first-degree murders are premeditated homicides, but no premeditated homicides are actions performed in self-defense, so it follows that no actions performed in self-defense are first-degree murders.

---

Submodule 6.3 Quiz

Licenses and Attributions

Key Sources:

• Watson, Jeffrey (2019). Introduction to Logic. Licensed under: (CC BY-SA).
• Content from http://www.philosophypages.com/lg/e08b.htm, http://www.philosophypages.com/dy/f9.htm , http://www.philosophypages.com/lg/e08a.htm, ; The Philosophy Pages by Garth Kemerling are licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.

Next Page: 6.4 Practice with Universals and Existentials