6.1 Existentials and Universals with Venn Diagrams
Venn Diagrams can be used to represent Existential (SOME) and Universal (ALL) claims. They can then be used to determine whether or not Categorical Syllogisms are valid.
Table of Contents
- 6.1 Existentials and Universals with Venn Diagrams
6.1.1 Existential and Universal Claims

Plato and Aristotle made important contributions to Categorical Logic.
Categorical Logic
We’re now beginning our study of Categorical Logic. We will be studying two kinds of claims in categorical logic: existentials and universals. An existential is a claim that a member of some category exists, and a universal is a claim that every member of a category has some property. Existentials and universals are sometimes called quantifiers, because they tell us how many members of a category are members of another category. They are also sometimes called generalizations, because they don’t inform us about any specific member or the category, only about some or all members of the category. A particular member of a category is sometimes called an instance or instantiation of that category. For instance, Felix the cat is an instance of the property of being a cat, whereas “some cats eats food” is a generalization about cats rather than a claim about any specific cats.
Existentials (SOME)
An existential claim is a claim that at least one member of a first category is a member of a second category. SOME Fs are Gs is true if and only if at least one F is also a G.
e.g., “Some dogs are homeless” is true if and only if at least one thing which is also a dog is homeless. “Some cats have rabies” is true if and only if at least one thing which is a cat also has rabies.
Explanation: Existential claims are a very common type of claim. Sentences using words like “some”, or “Somebody”, or “Something” are usually existential claims. For instance, “Something stopped the rain” or “Somebody turned off the music” are existentials.
“Something on the stove is burning” is true if and only if there exists something which is both on the stove and burning. There could be other things on the stove which aren’t burning, and there could be other things burning which aren’t on the stove. What matters is whether one of the things on the stove is burning.
“There is a sandwich on the table” is true if and only if a sandwich exists, a table exists, and the sandwich is on the table. Again, there could be other sandwiches on the floor, or other tables without sandwiches on them, or other things on the table besides sandwiches, like maybe a lamp. These are irrelevant: what matters is whether there is a sandwich on the table.
An existential claim that “Some F is G” is equivalent to a series of disjunctions for all members of the category F:
F1 is G v F2 is G, v F3 is G v . . . etc.
For instance, the claim that “some cats have no tails” is equivalent to the claim for all members of the set of cats {Cat1,Cat2,…} that:
Cat1 has no tail, or Cat2 has no tail, or Cat3 has no tail, or . . . etc.
The disjunction is true so long as at least one disjunct is true, and at least one of the Cats in the set has no tail. Similarly, an existential is true so long as at least one member of the category has the property ascribed to it.
Universals (ALL)
A universal claim is a claim that every instance of something has some property. “ALL Fs are Gs” is true if and only if there are no Fs which are not G.
e.g., “Everybody at the party is sad” is true if and only if nobody at the party isn’t sad. “All of the wells are tainted” is true if and only if every single well is tainted.
Explanation: Universal claims tend to use words like “ALL”, “EVERY”, “EVERYTHING”, and “EVERYONE”. They claim that everything which is part of one category is also a part of a second category. For example, “All children get on my nerves” is a universal claim.
“Everyone at the Dentist’s office is scared” is true if every single person at the Dentist’s office is scared (including the Dentist!). There can’t be a single exception if the claim is going to be true. The statement is still true if there are people who are scared who are elsewhere, and it’s still true if there are people who aren’t at the dentist’s office who aren’t scared.
Note: universals are vacuously true when the first category is empty. Thus, “All unicorns have stripes” is vacuously true given that there are no unicorns.
A universal claim that “All F are G” is equivalent to a series of conjunctions for all members of the category F:
F1 is G, & F2 is G, & F3 is G, & . . . etc.
For instance, the claim that “all cats have tails” is equivalent to the claim for all members of the set of cats {Cat1,Cat2,…} that:
Cat1 has a tail and Cat2 has a tail and Cat3 has a tail, and . . . etc.
The conjunction is true only if every conjunct is true, and false if there is any Cat in the set which has no tail. Similarly, the universal is true only when every member of the category has the property ascribed to it, and false if there is even one exception.
Using Capital Letters as Abbreviations
In the previous module, we used capital letters to represent whole declarative sentences. For instance:
S = “Shawn sheared the sheep.”
In this module, we will use capital letters to represent only predicates or categories into which some specific thing might fall. For instance:
S = “sheared the sheep”.
Here, S is no longer a complete sentence. We will use lowercase letters to represent particular things, and the word ‘is’ or ‘are’ will represent that the particular is a member of that category. So:
s = Shawn
S = “sheared the sheep”
s is S = “Shawn sheared the sheep”
A clue that a capital letter is abbreviating only a predicate or category, rather than a whole sentence, is that either the word ‘is’ or ‘are’ appears beforehand, or a quantifiers like ‘some’ or ‘all’ appears beforehand. When we write ‘some’ or ‘all’ followed by a predicate, followed by ‘is’ or ‘are’ and another predicate, we mean that some or all of the things in the first category fall into the second category. For instance:
S = has been sheared
P = sheep
Some P are S = “Some sheep have been sheared.”
All P are S = “All sheep have been sheared.”
6.1.2 Modeling Existentials with Venn Diagrams

‘X’ indicates that something exists within the circle.
Basic Venn Diagrams
We represent categories using Venn Diagrams. A circle represents a Category. For instance, we might draw a circle to represent Sports, and a circle to represent Safe Activities.
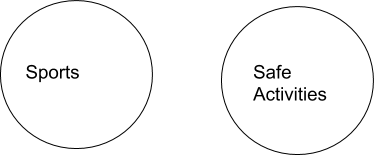
Anything that qualifies as a sport would fall into the circle “Sports”, whether hockey, lacrosse, soccer, football, volleyball, or curling. Anything that is a safe activity would be in the circle of “safe activities”, such as sitting or doing crossword puzzles. Sleeping would not be in the circle of sports, and fighting with swords would not be in the circle of safe activities. Existential claims are represented by an ‘X’ in the circle. For instance, the sentence “There are some safe activities” would be represented by:
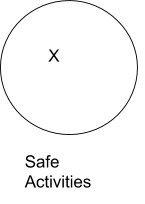
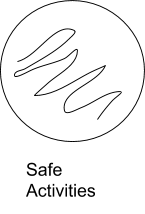
A category can be empty. We use shading or lines to represent that nothing falls into a category. Think of the shading like a “Black Hole” which indicates that something is empty (not that it is full). For instance, “There are no safe activities” would be represented by:
Shading all other areas in a Venn Diagram means that the unshaded space contains everything. For instance, here is how we would represent the claim that “Everything is a sport”, or, more literally, that “There is nothing which is not a sport.”
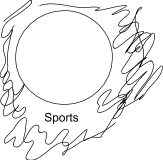
.
Existentials with Two Circles
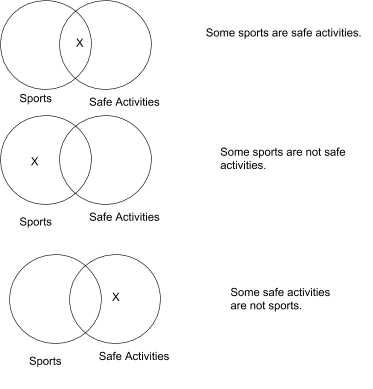
When two circles overlap, their intersection (the space where they overlap) represents anything which falls into both categories, and the area of each circle which doesn’t overlap with the other represents anything that falls into that category but not the other. There are two basic types of existentials:
Particular Affirmative: Some S are P (These are called “I” sentences)
Particular Negative: Some S are not P (These are called “O” sentences)
Below are Venn Diagrams for a particular affirmative and two particular negatives:
Existentials with Three Circles
When three circles overlap, the same principles apply: the overlap between any two or three circles represents what falls into those two or three categories, and anything in one circle but not another represents what falls into that category but not the other. Venn Diagrams with three circles are especially useful for representing arguments, as we will see soon. Here are some examples of existential claims that might be represented with three circles:
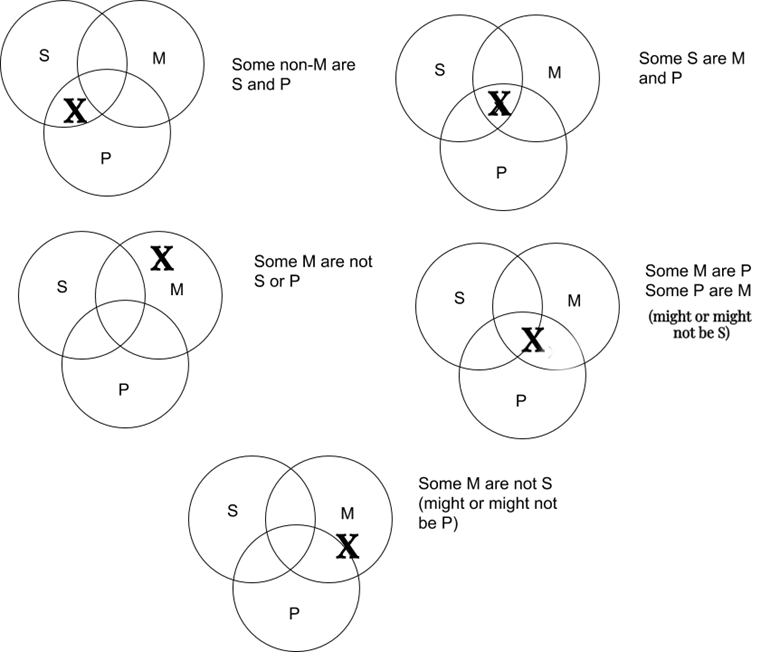
Important Note on the bottom circle: suppose that we know that something is in M which is not in S, but we don’t know whether or not it is in P. We then put it on the boundary of the circle for P within M that is outside of S. Similarly, notice that in the lower of the two circles on the right hand side, the ‘X’ goes in both M and P, but on the border of S, since “Some M are P” doesn’t tell us whether it is in or outside of S.
6.1.3 Modeling Universals with Venn Diagrams
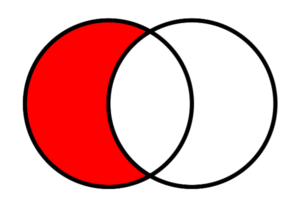
Shading represents that nothing is in the shaded area.
Universals with Two Circles
Recall that shading or scribbling in a region of a circle represents that there is nothing in that region of the circle. When two circles overlap, if their intersection is shaded, that indicates that nothing in the one category is a member of the other. This is called a universal negative.
Universal Negative: No S are P (These are called “E” sentences)
For example:

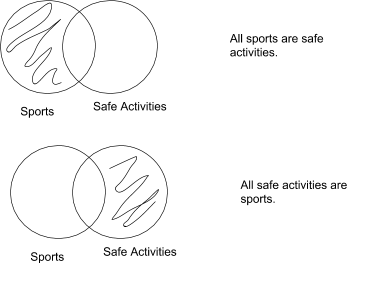
When the parts of a circle outside of the intersection are shaded, that indicates that nothing in that category is not in the other category.

A double negative is logically equivalent to a positive statement, so “No S are not P” is logically equivalent to “All S are P”. In other words, shading all of the other parts of a circle, so that the only white space is in other circle, indicates that everything in one category is a member of the other. This is called a Universal Affirmative claim.
Universal Affirmative: All S are P. (These are called “A” sentences)
For example:
Contradictory Claims: The Square of Opposition
Notice that some universals contradict some existentials. There can’t both be an ‘X’ in some region of a Venn Diagram, and also shading in that same region. There can’t be both something and also nothing in a region.
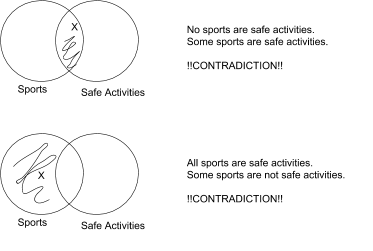
Notice that a Universal Negative is contradictory to a Particular Affirmative: it can’t both be true that No S are P and also that Some S are P. Likewise, a Universal Affirmative is contradictory to a Particular Negative: it can’t both be true that All S are P and that Some S are not P. The relationship between contradictory claims is called the “Square of Opposition”. While first described by Aristotle, we will use the modern, Boolean square of opposition in this class. Here it is:
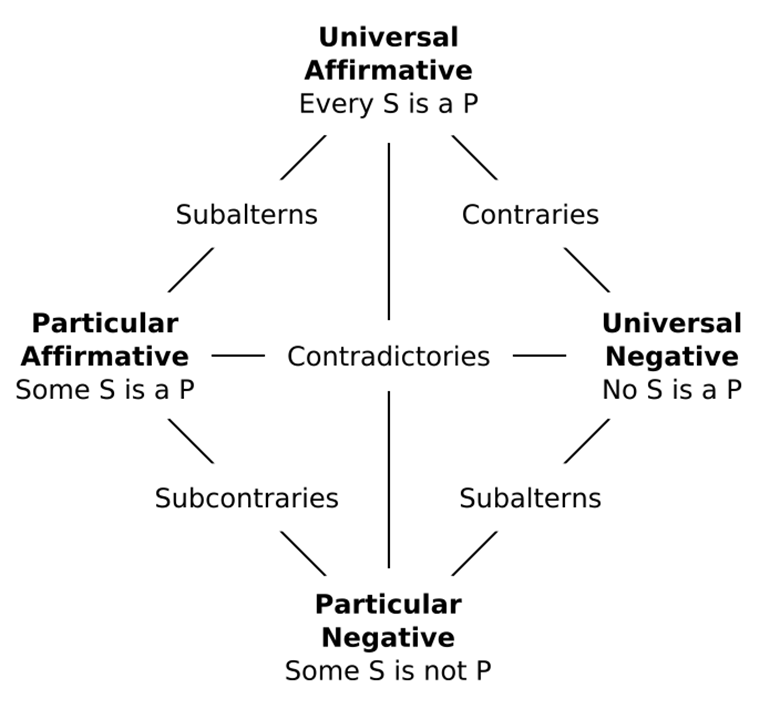
[Source: https://commons.wikimedia.org/wiki/File:Square_of_opposition.png]
Here is the same square of opposition using Venn Diagrams:
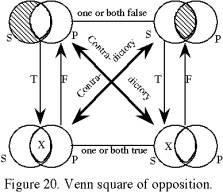
Universals with Three Circles
The same principles apply with universals that have three circles: shading indicates that there is nothing in that region of the diagram. Here are a few examples:
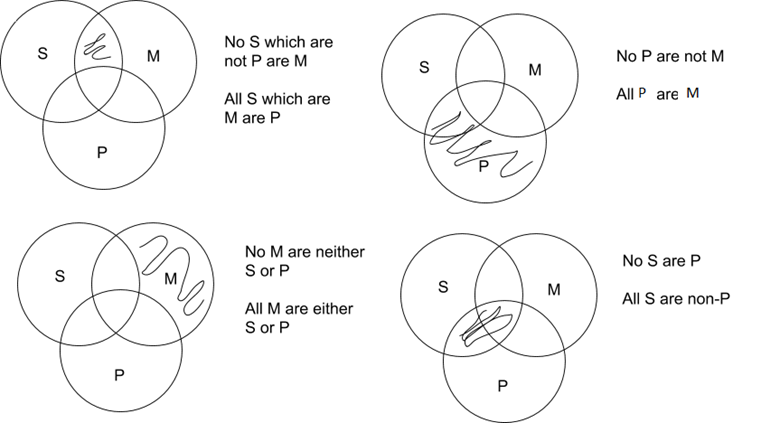
6.1.4 Using Venn Diagrams to Prove Validity
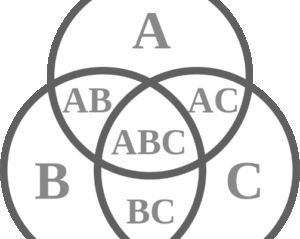
There are seven regions in a Venn Diagram with three circles.
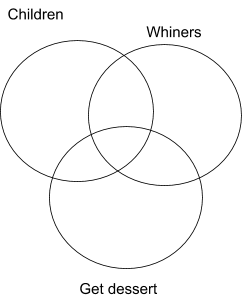
Step 1: Create the Venn Diagram
We can use a Venn Diagram with three circles to demonstrate the validity of certain types of categorical syllogism. A categorical syllogism is a specific form of argument where three categories are represented in a pair of premises, and two of those categories appear in the conclusion. The first step is to create a Venn Diagram for all of the categories represented in the argument. Let’s use this example:
- Some children are whiners.
- No whiners get dessert.
- Some children do not get dessert.
Three categories are represented in the argument: children, whiners, and getting desert.
Step 2: Diagram any Universal Claims in the Premises
Next, we diagram any universal affirmative or universal negative claims in the premises. Premise 1 is a particular affirmative, but Premise 2 is a universal negative, so we should diagram the universal negative:
“No whiners get dessert”
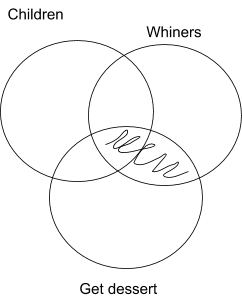
Notice that we shade in both areas where ‘Whiners’ and ‘Get Dessert’ intersect, both the area which also intersects with ‘Children’ and the area which does not.
Step 3: Diagram any Particular Claims in the Premises
Next, we add to the diagram any particular claims made in the premises. Premise 1 is a particular affirmative:
“Some children are whiners”
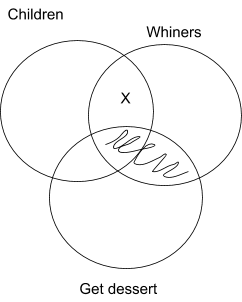
We need to draw an ‘X’ in the intersection of ‘Whiners’ and ‘Children’ to represent this claim. Because the intersection of ‘Whiners’ and ‘Children’ with ‘Get Dessert’ is already shaded in, indicating that nothing can be there, we have to place the ‘X’ in some open and empty space: the space where ‘Children’ and ‘Whiners’ intersect which falls outside of ‘Get dessert’.
Step 4: See if the Conclusion must be true given the Diagram
Lastly, we want to check and see if the conclusion must be true given the diagram. We don’t just want to see that the diagram is compatible with the conclusion, so that the conclusion might be true. For the argument to be valid, the diagram must guarantee that the conclusion is true. Our conclusion says:
“Some children do not get dessert.”
This is a particular negative claim. So, we should expect to see an ‘X’ somewhere which is inside the circle of ‘Children’, but outside the circle of ‘Get dessert’. In fact, that’s exactly what we see:

So, the argument is valid.
Suppose that instead the conclusion had been, “No children get dessert”. Then, we would need to see all of the intersection of ‘Children’ and ‘Get Dessert’ shaded in. But while “no children get dessert” is compatible with this diagram, the diagram doesn’t entail that it is true, because part of the intersection of ‘Children’ and ‘Get dessert’ is simply blank. So, the argument would not be valid with that conclusion.
Important Notes
These Venn Diagrams have three circles representing 3 categories, but each premise informs us about only 2 categories. When a premise is a particular affirmative (some S are P) or particular negative (some S are not P), then there is not enough information in the premise itself to determine whether the ‘X’ should go within or outside of the third category. For this reason, the ‘X’ needs to be written on the line of the circle not represented in the premise whenever it is unclear whether the X is inside or outside of it. For instance, consider this argument:
1. Some cows are animals.
2. Some animals are not birds.
C. Some cows are not birds.
Here, premise 1 tells us that an ‘X’ needs go in the intersection of both ‘cows’ and ‘animals’, but it isn’t clear whether or not that ‘X’ should go in birds, so we should draw it on the border of ‘birds’. Premise 2 tells us that an ‘X’ should go in ‘animals’ outside of ‘birds’, but it doesn’t tell us whether that X belongs inside or outside of the circle for ‘cows’, so it should go on the border of ‘cows’.
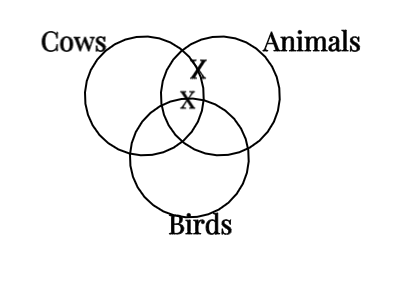
An ‘X’ in the intersection of circles labelled ‘cows’ and ‘animals’, but on the border of ‘birds. A second ‘X’ in Animals and outside of birds, but on the border of ‘cows’.
If an area is shaded, then no X can be written in it. This is why it is important to remember to do universal premises before you do particular premises. Since universal premises involve shading some part of a circle, that can tell us whether an X does or does not go in that part of the circle. For instance, consider this argument:
1. No cows are birds.
2. Some animals are cows.
C. Some animals are not birds.
Here, premise 1 tells us that nothing is in the intersection of cows and birds. On its own, premise 2 only tells us that there is an ‘X’ in the intersection of ‘cows’ and ‘animals’, but it doesn’t tell us whether that ‘X’ goes in ‘birds’ or not. However, premise 1 tells us that nothing is both in ‘cows’ and ‘birds’, so we know the ‘X’ goes outside of birds.
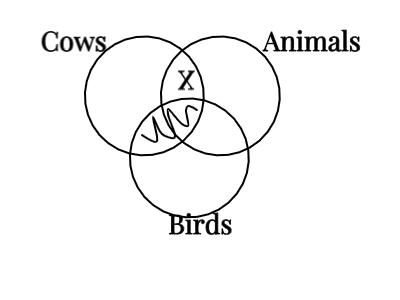
Three circles: shading in the intersection of ‘cows’ and ‘birds’, an ‘X’ in the intersection of ‘cows’ and ‘animals’ but outside the shaded part of ‘birds’.
Submodule 6.1 Quiz
Licenses and Attributions
Key Sources:
- Watson, Jeffrey (2019). Introduction to Logic. Licensed under: (CC BY-SA).
Next Page: 6.2 Rules for Universals and Existentials
