1.2 Formal and Informal Logic
An argument is a structure of “premises”, or reasons, followed by a conclusion inferred from those premises. Informal Logic studies general guidelines for good argumentation, the habits of a good reasoner, or “intellectual virtues”, and the tendencies we have to make mistakes in reasoning, or “fallacies”.1.3 The Standard View
Formal Logic studies abstract patterns of reasoning that meet the strictest standard for argumentation – validity. An argument is valid when there is no possibility of the premises being true with the conclusion false.
Table of Contents
- 1.2 Formal and Informal Logic
1.2.1 Informal Logic

Fallacies are like breaks in a chain of reasoning.
Formal and Informal Logic
The subjects studied in a logic course are usually divided into informal logic and formal logic. Informal logic is the study of general guidelines for good reasoning, rather than strict rules, and it tends to focus more on real-world examples where reasoning succeeds or fails. Formal logic is the study of abstract patterns of reasoning that meet the strictest standard for arguments, called validity, so that any argument which follows the pattern is guaranteed to have a true conclusion if its starting assumptions, or premises, are true. We will begin and end this course with topics in informal logic, and spend the middle of the course studying formal logic. Both are useful tools for improving your own reasoning.
Informal Logic: Intellectual Virtues
Our study of informal logic will focus on intellectual virtues, which are character traits or dispositions which tend to help reasoners to arrive at the truth. Because the best way to arrive at true beliefs will differ from situation to situation, intellectual virtues are not strict rules, and they do not always guarantee that someone will believe the truth. Instead, they describe a range of attitudes which a good reasoner might develop. For instance, someone who wants to have true beliefs ought to be someone who tends to believe what they have more evidence for, rather than what they have less evidence for. Sometimes this will fail, however, because sometimes we can have a lot of misleading evidence: a jury might convict an innocent person on the basis of evidence, for example, if the evidence was manufactured to frame the person for a crime they didn’t commit. In spite of this, tending to form beliefs in accordance with the evidence is a good intellectual virtue to develop.
Informal Logic: Intellectual Vices
The opposite of an intellectual virtue is an intellectual vice. An intellectual vice is a tendency which most often leads reasoners away from the truth rather than towards it. For example, a person who is very fearful might tend to form beliefs based on what they most fear or dread happening, rather than on the basis of their evidence. This person will tend to form false beliefs and take irrational actions, like refusing to fly on planes or buying an excessive amount of life insurance. On the other hand, a person might suffer from the opposite vice, overconfidence. An overconfident person might ignore the evidence of danger, and engage in excessively risky behaviors. Both of these are intellectual vices, because they tend to lead to false beliefs.
Informal Logic: Fallacies
Intellectual vices tend to lead to problematic arguments, or fallacies. Fallacies are patterns of mistakes in reasoning that humans are especially inclined to make. Fallacies often look very similar to good arguments on the surface, but on closer inspection they are not properly aimed at the truth. One of the things you will study in this class are dozens of recognized fallacies which philosophers and logicians have identified over the years.
For instance, it’s well-recognized that people tend to believe something if a lot of people around them believe the same thing. Usually this is a good strategy for forming beliefs, because if the people around us are likely to have better evidence about something than we are, then believing what they believe will tend to lead us to true beliefs. If you haven’t been outside lately, but everyone around you says that it is raining outside, and they have been outside recently, then it is probably raining outside. Sometimes, however, the people around us are not more likely to have better evidence about something than we are. For instance, if someone has a rare medical condition, and most people around him suggest treating it with chicken soup and bed-rest, it would be a fallacy for him to conclude, “chicken soup and bed-rest is the solution” on the basis of other people saying so.
There is no single, unified list of all possible fallacies. There is no limit on the number of ways we go wrong! Instead, we will learn about fallacies by studying specific ways that humans tend to go wrong, and by studying the intellectual virtues that one can develop to try to avoid these mistakes.
1.2.2 Arguments

An argument is a series of premises followed by a conclusion.
Arguments in Standard Form
We have already discussed that reasoning is the process of arriving at a conclusion on the basis of some reasons or evidence which make that conclusion likely to be true. The process of arriving at a conclusion on the basis of reasons is called an inference. For example, I might infer (that is, make an inference) the conclusion that I am coming down with a cold on the basis of the evidence that my sinuses feel congested. We can model inferences as formal arguments. A formal argument is a numbered list of premises, followed by intermediate steps or inferences that follow from those premises, followed by a conclusion. For example:
- My sinuses feel congested. (Premise 1)
- If my sinuses feel congested, then either I have a cold or I have allergies. (Premise 2)
- Either I have a cold or I have allergies. (follows from 1 and 2)
- I don’t have allergies. (Premise 3)
C. I have a cold. (follows from 3 and 4)
Lines 1, 2 and 4 are called premises, which are the reasons that we used to arrive at our conclusion. Line 3 is an intermediate inference. An intermediate inference is something inferred from earlier lines or premises in an argument, which is then used to infer later lines or the conclusion of an argument. The parentheses note that line 3 follows from line 1 and line 2. We labeled the conclusion “C”, although we might have numbered it “5”; this choice doesn’t make a difference. The parentheses note that the conclusion follows from lines 3 and 4. Notice that the reasoning in our argument goes from top to bottom, step by step, never backwards (we can’t infer line 2 from line 3).
Laying out arguments in this way, to make clear the premises and the conclusion, is called putting arguments into Standard Form. Putting arguments in Standard form is a tool used in both informal and formal logic. Categorical Logic and Propositional Logic can have different rules for what else is required for “Standard” Form: for instance, Categorical Logic requires for “Standard Form” that the predicate of the conclusion occur in the first premise, that the subject of the conclusion occur in the second premise, and that the first and second premise share some ‘middle term’ in common. Propositional Logic doesn’t require this. But the distinction between premises and conclusion is a very useful one for a lot of purposes!
In particular, by identifying the premises of an argument, we can know what in the argument can be challenged, and what in the argument needs to be defended. If someone wanted to challenge the conclusion (C), that I have a cold, then they would need to challenge one of the premises on line (1), (2) or (4). They would need to give a reason to think that the premise was false. For example, they might say that premise 3 is false, because I’ve overlooked another reason my sinuses might be congested, such as a sinus infection. Defending an argument requires defending the premises. We will study near the end of this class ways of defending the premises of an argument, including using analogies, using probability, and using induction.
1.2.3 Formal Logic

Like shapes or patterns, two arguments can share a form, yet differ in content.
Formal Logic
Formal logic studies rules and principles that apply to the abstract form of an argument, independent of its content. What do we mean by the “form” of an argument?
Consider the following argument in Standard Form:
1. My sinuses feel congested. (Premise 1)
2. If my sinuses feel congested, then either I have a cold or I have allergies. (Premise 2)
3. Either I have a cold or I have allergies. (follows from 1 and 2)
4. I don’t have allergies. (Premise 3)
C. I have a cold. (follows from 3 and 4)
Now, consider an argument about something completely different:
1. Gabby has a pet goat. (Premise 1)
2. If Gabby has a pet goat, then either she bought the goat, or she stole it. (Premise 2)
3. Either Gabby bought the goat, or she stole it. (follows from 1 and 2)
4. Gabby didn’t buy the goat. (Premise 3)
C. Gabby stole the goat. (follows from 3 and 4)
These arguments are about completely different topics. Goat thieves and sinus problems have nothing in common. The content of the arguments is completely different.
At the same time, you’ll notice that there is something similar about the two arguments, though. What is similar about them is called their form. Both arguments have the same form. Formal Logic involves abstracting away from the subject matter or content of the argument, and focusing on the form. Here is the form which both arguments have in common. We will use capital letters X, Y, and Z here to represent sentences:
1. X
2. If X, then either Y or Z.
3. Either Y or Z (from 1, 2)
4. Not Y
C. Z (3,4)
Look closely, and you will notice that both arguments follow this same form. Formal logic studies the form, rather than the content.
1.2.4 Validity

We can know an argument is valid based on its form alone.
Image Credit: Kalinka Anguelov CC 4.0
Validity
Formal logic is the study of abstract forms of argument. Some forms of argument are valid, and some forms of logic are invalid. We can know that some arguments are valid simply by looking at their form, without even considering their content.
A valid argument is one where there is no possibility of the premises being true with the conclusion being false. In other words, if the premises are true, then the conclusion would have to be true. If someone knows the premises are true, and they know that the argument’s form is valid, then they know that the conclusion has to be true. Formal logic studies those forms of argument which have been shown to be valid, no matter what the subject matter or content someone sticks in the argument. The form of argument above in our example is valid. You can test this yourself! Replace ‘X’ with any sentence you like, ‘Y’ with any other sentence you like, and ‘Z’ with any third sentence you like. The result might be silly, but it will be valid.
An invalid argument, then, is an argument with a counterexample. A counterexample to an argument is a possible scenario where all of the premises might be true and, at the same time, the conclusion might be false. A counterexample can be hypothetical, it doesn’t have to actually be the case. An argument is invalid if there is a counterexample: that is, if there is a possible situation where each of the premises is true and the conclusion false. For example, this argument is invalid:
- Fred’s clothes were more expensive than Dan’s clothes (Premise)
- Dan’s clothes are unfashionable. (Premise)
- Fred’s clothes are fashionable (From 1, 2)
You don’t have to know anything about Fred, Dan, or their clothing choices in order to know that this argument is invalid. Line 3 does not follow from lines 1 and 2. This is because there is a possible scenario where both premise 1 and premise 2 are true — Dan’s clothes are unfashionable, and Fred’s clothes are more expensive — but the conclusion is false, and Fred’s clothes are not fashionable. For instance, it might be that Fred’s clothes were unfashionable but overpriced; it might be that paying more doesn’t guarantee being fashionable. We can know that this is a hypothetical possibility, even if we don’t know whether 3 is true or false, or whether 2 is true or false. Even if the conclusion of an argument is true, it can still be invalid, if there is a possibility that the conclusion might be false with the premises true.
Every invalid argument can be made valid by the addition of the right premises. Later in the course we will study how to make invalid arguments into valid arguments. For example, the following argument would be valid, although the premise we would have to add to the argument is probably false:
- Fred’s clothes were more expensive than Dan’s clothes (Premise)
- Dan’s clothes are unfashionable. (Premise)
- If Fred’s clothes were more expensive than someone’s unfashionable clothes, then Fred’s clothes are fashionable. (Premise)
- Fred’s clothes are fashionable (From 1, 2, 3)
Most arguments that people make are invalid. We will spend much of the course learning how to turn the invalid arguments we make into valid arguments. But even when an argument is valid, that doesn’t mean it is a “good” argument. An argument can fail in an another important way: the premises might not be true! Validity doesn’t mean that the premises are true, it means that if the premises were true, the conclusion would have to be true.
We use the term sound to mean an argument that is (i) valid and (ii) the premises are true. An invalid argument can’t be sound, because an argument must first be valid in order to be sound. But a valid argument can be unsound, because even though structurally the premises guarantee the conclusion, the premises themselves are false. Validity is about the “form” of an argument (could the conclusion be false if the premises were true?), soundness is about not just the form but also the “content” (is it true or false).
A good argument should be not just valid, but sound. It is much harder to evaluate the truth of the premises of an argument, though, so we’ll spend the first two-thirds of the course simply focusing on the structure of arguments (validity) and only later getting to questions of how to evaluate the evidence for the premises (soundness). Some arguments always are valid, but never sound, like arguments with contradictory premises (the premises can’t possibly be true). Arguments which have a conclusion which is a necessary truth (a statement that can’t possibly be false) valid on our definition even when the premises are irrelevant to the conclusion. So, validity is not a concept which captures all there is to being a good argument. Still, validity is the most important first step in logic!
1.2.5 Tools of Formal Logic

John Venn (1834-1923) was an English logician who invented the Venn Diagram.
Tools of Formal Logic
Formal logic gives us the tools to quickly and consistently determine whether or not an argument is valid or invalid, and to know how to repair an invalid argument. Formal logic does this by abstracting away from the particular content of an argument and paying attention only to its form. We will spend much of this class learning to use four tools from formal logic: Venn Diagrams, Symbolization, Rules of Inference, and Truth tables.
Venn Diagrams
One formal method which you might already be familiar with from other classes is called a venn diagram. Venn Diagrams are used in categorical logic. A Venn Diagram looks like this:
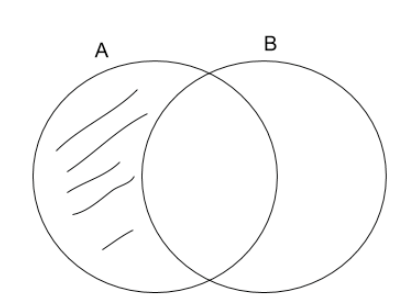
Lines indicate that nothing is in that section of the Venn Diagram; white space indicates that something could be in that section of the Venn Diagram.
A and B stand for categories into which things can be classified. This diagram indicates that all As are Bs. The lines indicate that nothing is in that section of the Venn Diagram, or that nothing is in A that is not in B. The empty space represents that something could be in that section of the diagram: some As might be Bs. For example, A might stand for the category “Children”, and B might stand for the category of “Valuable Things”, and so this diagram would indicate that no children are not valuable; that is, that all children are valuable. We will learn how to use Venn Diagrams to determine whether or not an argument is valid.
Truth Tables
| P | Q | P or Q | not-P | Q |
| True | True | True | False | True |
| True | False | True | False | False |
| False | True | True | True | True |
| False | False | False | True | False |
Another formal method we will learn how to use is called a truth table. Truth tables are used in propositional logic. A truth table is a way of coming up with a complete list of all of the possible scenarios, in order to determine whether an argument is valid or invalid. A truth table looks like this:
Here, P and Q each stand for sentences, and the rows of the truth table stand for possible truth values of those sentences. There are four possible combinations of the truth tables of P and Q.
For example, suppose P stands for “Mary likes John”, and Q stands for “John Likes Mary”. The rows of this truth table describe four possible scenarios:
- Mary likes John and John likes Mary (row 1)
- Mary likes John but John doesn’t like Mary (row 2)
- Mary doesn’t like John, but John likes Mary (row 3)
- Mary doesn’t like John, and John doesn’t like Mary (row 4)
The columns of the truth table then indicate for certain complex sentences whether the sentence would be true or false in that scenario. We will later learn how to create truth tables and use them to determine whether or not an argument is valid or invalid.
Symbolization
Another tool we will be learning to use is called symbolization. As you’ve noticed above, using letters like A or B or P or Q makes logic look very abstract, almost like mathematics. We will also introduce symbols for some common logical connectives, like the & symbol for ‘and’. For instance, we might symbolize “John is tired and hungry” as T & H, where T = “John is tired”, and H = “John is hungry”.
This might look intimidating if you don’t like mathematics, but we do this for a practical purpose. Symbolizing sentences helps us ignore the content and focus on the form of the sentence, and that helps us to recognize the form of an argument made up of those sentences. Remember, it is the form which can most easily tell us that an argument is valid. We will learn how to translate from English into symbolic logic, and from symbolic logic into English. Like learning a new language, this means learning logic requires a lot of intense practice at first, but eventually becomes natural.
Rule of Inference
The last and most important tool we will be learning is called a rule of inference. The rules of inference we will learn are fixed patterns than an argument or inference can follow which is always valid. For example, this pattern is always valid:
1. Either Y or Z
2. Not Y
C. Z (1,2)
This pattern is called disjunctive syllogism. The name might sound like quite a mouthful! The name itself is not so important. What matters is that by giving names to some of the most important and useful patterns and memorizing these rules, we’ll be able to quickly verify that an argument which correctly applies the rules is valid, and we’ll know what needs to be added to an invalid argument in order to make it valid.
We’ll learn many rules in this class, and you’ll likely want to memorize the most important rules. The more you are able to internalize the rules and think in terms of the rules, the more readily you will be able to incorporate logic into everyday life. For now, just be prepared to learn rules of inference.
Applications of Formal Logic
Near the end of the course, after we have finished studying Formal Arguments, we will turn back to studying the content of arguments, and how to evaluate whether premises are true or false in the real world. This will require us to study other tools like statistics and probability, the nature of analogies, the use of induction and the development of a scientific hypothesis, and the structure of claims about cause and effect. These tools help us determine whether premises are likely to be true, or whether we should believe them, rather than whether arguments are valid or invalid. You will learn more about each of those later; for now, just know that at the end of the class we will see how to apply all of these abstract tools to concrete questions that need to be answered. We will end the class by thinking about some of the responsibilities that those who have learned logic have to encourage others around them to engage in better reasoning.
Submodule Quiz
Licenses and Attributions
Key Sources:
- Watson, Jeffrey (2019). Introduction to Logic. Licensed under: (CC BY-SA).
Multimedia:
- John Venn (1834-1923) Venn Diagram. Licensed under: (CC BY).
Next Page: 1.3 The Standard View
